0

I am quite new to using tikz and the pgf package in general, and I'm having a hard time understanding how/when to use pgfmathsetmacro, pgfmathparse and pgfmathresult. I have the following problem: I am trying to define a command for a linear transformation that I want to use inside TikZ. The transformation is given by

enter image description here

I thought about defining a command that takes an input argument and predefined values of a, b, c and d and returns the mapped coordinate, which I will then use in a \coordinate definition. Here is a MWE:

\documentclass[]{standalone}
\usepackage{tikz}

\begin{document}
\usetikzlibrary{math}


% Define mapping coordinates to map [a,b] -> [c,d]. Do it separately for x and y
\tikzmath{\ax = 1; \bx = 2;
          \ay = 1; \by = 2;
          \c = 0;  \d = 1;}


% Define the transformation as a new command that uses pgf's math engine. It takes 1 input argument
% I don't know how to define this properly, it does not give me any error but I think it is wrong
\newcommand{\transformX}[1]{\pgfmathparse{((\c+\d) + (\d-\c)((2{#1} - (\ax+\bx))/(\bx-\ax)))/2}\pgfmathresult}
\newcommand{\transformY}[1]{\pgfmathparse{((\c+\d) + (\d-\c)((2{#1} - (\ay+\by))/(\by-\ay)))/2}\pgfmathresult}


\begin{tikzpicture}[x=1in,y=1in]
    \coordinate (myCoord) at (\transformX{1.5},\transformY{1.4}); % error
\end{tikzpicture}
\end{document}

I thought that pgfmathsetmacro, pgmathparse or functions alike should do the trick, but I do not know how to implement them. I read this post and this post (the latter I believe is very similar to what I'm trying to achieve) but I could not adapt to my case.

Any ideas on what to do? Thanks!

Pedro Montanari
  • 1
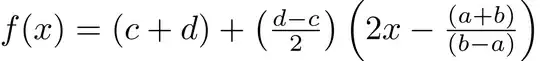
  • The main deficiency of pgfmath is its lack of expandability. I'd generally use the nowadays LaTeX built-in floating point capabilities. That is, replacing \pgfmathparse with \fpeval and removing \pgfmathresult. – AlexG Feb 16 '24 at 15:43
  • Thanks @AlexG this actually worked for me! I am trying to understand the concept of "expandability" as I've seen in other posts. I was actually trying to use \transformX{1.5+0.5} and it did not work. However, using \transformX{\fpeval{1.5+0.5}} worked. From this I understand that "expandability" means that the result of calculations is not evaluated directly if we don't ask LaTeX to do so. Is that correct? Thanks again – Pedro Montanari Feb 16 '24 at 16:42
  • If you're doing more complicated mathematics, you should check out the sagetex package which gives you access to a computer algebra system. The problem here shows how sagetex can do the calculations for tikz. The post here shows how Sage can handle calculations that LaTeX is just not designed to solve. – DJP Feb 18 '24 at 23:45

0 Answers0