Tikz automatically computes the bounding box of the graphical elements in a picture which determines its overall final size.
The size of the axis box projected on the canvas changes when viewed from different angles which results in the observed "pumping".
A way to work around this issue is to place a graphical object that does not change its 2d projection on the canvas when rotated and which encompasses all parts of the plot. Most suitable for this purpose is the bounding cylinder whose axis aligns with the rotation axis.
Bounding cylinder hidden (draw=none):
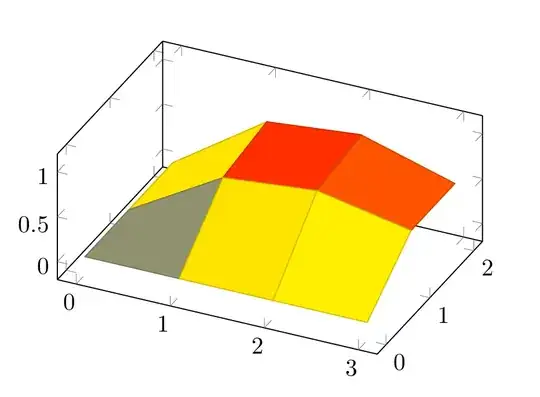
With cylinder shown:
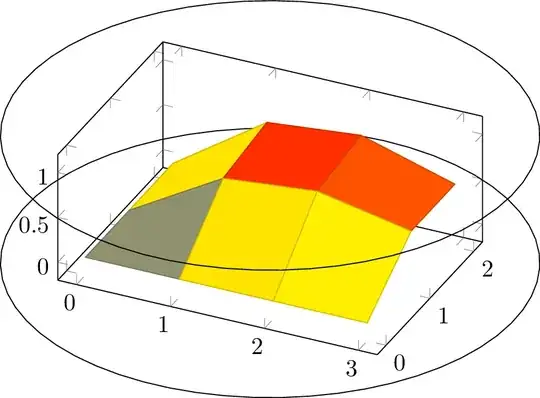
\documentclass[export]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usepackage{animate}
\begin{document}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% fix axes to these ranges (depending on the data to be plotted, of course)
\def\xmin{-0.2}
\def\xmax{3.2}
\def\ymin{-0.2}
\def\ymax{2.2}
\def\zmin{-0.2}
\def\zmax{1.2}
% bounding cylinder based on axes ranges with some scaling and z-offsets to also
% include tick labels
\def\scaleCylRadius{1.25}
\pgfmathsetmacro\cylCentreX{0.5(\xmin+\xmax)}
\pgfmathsetmacro\cylCentreY{0.5(\ymin+\ymax)}
\pgfmathsetmacro\cylRadius{\scaleCylRadiussqrt((\xmax-\xmin)^2+(\ymax-\ymin)^2))/2}
\pgfmathsetmacro\cylZMin{\zmin - 0.02}
\pgfmathsetmacro\cylZMax{\zmax + 0.0}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\begin{animateinline}[controls]{20}
\multiframe{60}{rAngle=25+6}{
\begin{tikzpicture}
\begin{axis}[
view = {\rAngle}{30}, % <-- Rotate View
unit vector ratio = 1 1 1,
trig format plots=rad,
xmin=\xmin,xmax=\xmax,
ymin=\ymin,ymax=\ymax,
zmin=\zmin,zmax=\zmax,
clip=false, % don't clip cylinder circles to axes ranges
]
% lower circle
\addplot3[
draw=none, % comment out to see cylinder circles
domain=0:2pi,samples=60]({\cylCentreX+\cylRadiussin(x)},{\cylCentreY+\cylRadiuscos(x)},\cylZMin);
% data
\addplot3[surf, mesh/rows=3] coordinates {
(0,0,0) (1,0,0) (2,0,0) (3,0,0)
(0,1,0) (1,1,0.6) (2,1,0.7) (3,1,0.5)
(0,2,0) (1,2,0.7) (2,2,0.8) (3,2,0.5)
};
% upper circle
\addplot3
draw=none,
domain=0:2*pi,samples=60;
\end{axis}
\end{tikzpicture}
}
\end{animateinline}
\end{document}



\useasboundingbox (0,0) circle[radius=10cm];) – hpekristiansen Mar 23 '22 at 23:14