So The Jacobi Elliptic Functions are a little bit tricky to plot because they depend on the complete elliptic integral of the first kind K(k) that can be written as a sum of double factorials, and the Fourier series for the Jacobi Elliptic Functions then depend on exponentials of these elliptic integrals, I can easily write all the mathematical formulas, but I don't know an easy way to represent them on Tikz or PGF, probably gnuplot would be the easiest but I would like to make it depend only on Tikz PGF because of configurations problems I am having with gnuplot, and I would like to write that in a formulaic form, instead of a table because I would like to change a parameter easily from one compilation to another.
Basically, is there a way to calculate summations and double factorials in Tikz - PGF on some variables and then use them in a plot of a function that will depend on those ?
Bassically I need a way of calculating:
K(k) = pi/2 sum[n=0:10] ((( 2 * n - 1)!!)/((2 * n)!!)) * (k^(2*n))
and for a given u and v= sqrt(1-u^2)
q = exp(-pi * (K(v)/K(u)))
calculate and plot for example:
sn_u(x) = (2* pi/(K(u) * u)) * sum[n=0:5] (((q^(n+0.5)) * sin((2*n+1) * x * pi/(2 * K(u))))/(1-(q^(2n+1))))
How do I implement these sums and double factorial as a function? Also is there a way to make these calculations modular in the way I wrote them?
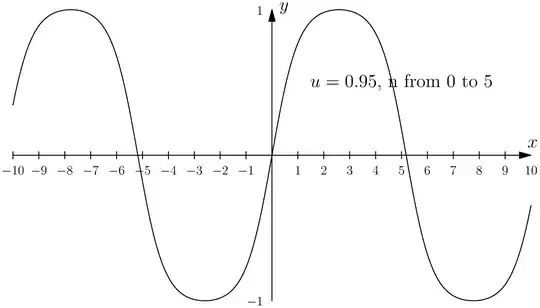
sn_u(x), https://imgur.com/rXpzMTX. – Nguyen Van Chi Jun 19 '22 at 11:47sn(x,u)that converges "fast" and "uniformily". The Desmos graph: https://www.desmos.com/calculator/kuymi4vh3k , sorry. – Felipe Dilho Jun 19 '22 at 18:19