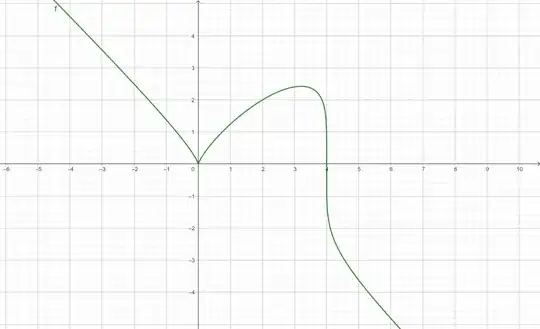
You've come to a point where you are seeing some of the limitations of mathematics in LaTeX. To be fair, LaTeX is for typesetting and you shouldn't expect it to take the place of Geogebra. This is an opportunity to assess how much complicated mathematics you will be using in LaTeX
otherwise the problem of graphing the 5th root today can become pgfplots: problem with convergence of addplot on (sin(x) - x cos(x)) / x^3. As I say in my answer there, "The sledgehammer that will solve most any problem is a computer algebra system (CAS). The sagetex package gives you access to an open source CAS called Sage as well as Python programming.". A CAS has a steeper learning curve but can solve more problems: integration, derivatives, differential equations, matrix inverses, graph theory, etc. and Python gives you a powerful programming language to replace some of the more dated LaTeX programming that many here have mastered.
Here is a sagetex solution to your problem:
\documentclass{article}
\usepackage{sagetex,xcolor,pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{sagesilent}
LowerX = -5
UpperX = 5
LowerY = -5
UpperY = 5
step = .01
t = var('t')
g(t)= real_nth_root(4*t^4-t^5, 5)
x_coords = [t for t in srange(LowerX,UpperX,step)]
y_coords = [g(t).n(digits=6) for t in srange(LowerX,UpperX,step)]
output = r""
output += r"\begin{tikzpicture}[scale=1.0]"
output += r"\begin{axis}[xmin=%f,xmax=%f,ymin= %f,ymax=%f,width=10cm,"%(LowerX,UpperX,LowerY, UpperY)
output += r"xlabel=$x$,ylabel=$y$,axis x line=middle,axis y line=middle]"
output += r"\addplot[thin, blue, unbounded coords=jump] coordinates {"
for i in range(0,len(x_coords)-1):
if (y_coords[i])<LowerY or (y_coords[i])>UpperY:
output += r"(%f , inf) "%(x_coords[i])
else:
output += r"(%f , %f) "%(x_coords[i],y_coords[i])
output += r"};"
output += r"\end{axis}"
output += r"\end{tikzpicture}"
\end{sagesilent}
\sagestr{output}
\end{document}
The output in Cocalc is:
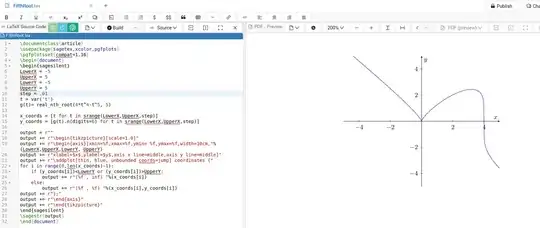
A brief explanation:
sagesilent environment is work behind the scenes that doesn't get printed until you tell it. LowerX = -5, UpperX = 5, LowerY = -5, UpperY=5 sets up the parameters of what will be on the screen, step = .01 sets up the spacing between x-values. g(t)= real_nth_root(4*t^4-t^5, 5) indicates the 5th root of your function will be graphed but since there are 5 such roots over the complex number field, we specify that the real valued answer will be used. x_coords = [t for t in srange(LowerX,UpperX,step)] creates a list of the specific x-coordinates that will be used: -5, -4.99, -4.98, ..., 4.99 (Python doesn't include the last number. You can modify to UpperX+step to go to 5.00). The y-coordinates get calculated using 6 significant digits. The picture is created as a text string because sagetex runs as a 3-step compilation process. If you search this site for sagetex you can find more explanation on this. \sagestr{output} takes the work created in sagesilent so that on the third step of compilation all the calculations/details from Python/Sage get typeset. The for-loop for i in range(0,len(x_coords)-1): checks that the y-value is on the screen. If it isn't the y-value is infinity and won't be plotted. Otherwise it will be plotted.
LaTeX, a CAS, and Python programming can help you solve and typeset most anything. However, the CAS Sage is not part of your distribution. The easiest way to access it is through a free Cocalc account. It's also possible to download Sage to your computer and get it to work with your LaTeX distribution. That takes more time and can be more problematic. It requires more maintenance as well: as Sage and LaTeX update on different schedules, that coordination can break. Working on Cocalc means they make sure everything stays up to date and works. If you don't need the mathematical power of a CAS then other solutions, such as lua, are probably more appropriate.