You need \tl_put_right:Nx so the argument is fully expanded. But you don't want to fully expand \mbox and \tiny, so a robust wrapper is needed. A command defined with \NewDocumentCommand is never expanded in e-expansion or x-expansion.
\documentclass[11pt]{article}
\usepackage{tikz}
\usetikzlibrary{matrix}
\NewDocumentCommand{\tinybox}{m}{\mbox{\tiny#1}}
\ExplSyntaxOn
\NewDocumentCommand{\indexprod}{ m } % indices
{
\seq_set_from_clist:Nn \l_tmpc_seq { #1 }
\int_step_inline:nn {\seq_count:N \l_tmpc_seq}
{
\seq_put_right:Nn \l_tmpa_seq {1}
\seq_put_right:Nn \l_tmpb_seq {1}
}
\int_step_inline:nn {\seq_count:N \l_tmpc_seq - 1}
{
\tl_put_right:Nx \l_tmpa_tl {\tinybox{$ \seq_item:Nn \l_tmpc_seq {##1} = 1$} &}
}
\tl_put_right:Nx \l_tmpa_tl {\tinybox{$ \seq_item:Nn \l_tmpc_seq {\seq_count:N \l_tmpc_seq} = 1$} \}
\int_new:N \l_tmpc_int
\int_new:N \l_tmpd_int
\int_set:Nn \l_tmpc_int {4}
\int_step_inline:nnn {2} {\seq_count:N \l_tmpc_seq}
{
\int_set:Nn \l_tmpc_int {\l_tmpc_int * 4}
}
\int_log:N \l_tmpc_int
\int_step_inline:nnn {2} {\l_tmpc_int}
{
\int_set:Nn \l_tmpb_int {##1}
\int_log:N \l_tmpb_int
\int_step_inline:nn {\seq_count:N \l_tmpc_seq}
{
\int_set:Nn \l_tmpa_int {\seq_item:Nn \l_tmpa_seq{####1}}
\int_set:Nn \l_tmpd_int { \int_eval:n {\l_tmpa_int + 1}}
\int_log:N \l_tmpd_int
\seq_set_item:NnV \l_tmpb_seq {####1} \l_tmpd_int
}
\seq_log:N \l_tmpb_seq
\int_step_inline:nn {\seq_count:N \l_tmpc_seq - 1}
{
\tl_put_right:Nx \l_tmpa_tl {\tinybox{$ \seq_item:Nn \l_tmpc_seq {####1} = \seq_item:Nn \l_tmpb_seq{####1} $} &}
}
\tl_put_right:Nx \l_tmpa_tl {\tinybox{$ \seq_item:Nn \l_tmpc_seq {\seq_count:N \l_tmpc_seq} = \seq_item:Nn \l_tmpb_seq {\seq_count:N \l_tmpb_seq}$} \}
\int_step_inline:nn {\seq_count:N \l_tmpc_seq}
{
\int_set:Nn \l_tmpa_int {\int_eval:n {\seq_item:Nn \l_tmpb_seq{####1}}}
\int_log:N \l_tmpa_int
\seq_set_item:NnV \l_tmpa_seq {####1} \l_tmpa_int
}
\seq_log:N \l_tmpa_seq
}
\begin{tikzpicture}[baseline={([yshift=-0ex]current~bounding~box.center)}]
\matrix(m) [
matrix~of~nodes,
ampersand~replacement=&,
column~sep=1ex,
nodes~in~empty~cells,
nodes={
shape=rectangle,
minimum~height=3ex,
anchor=center
},
]{
\tl_use:N \l_tmpa_tl
};
\end{tikzpicture}
}
\cs_generate_variant:Nn \seq_set_item:Nnn { NnV }
\ExplSyntaxOff
\begin{document}
[
\indexprod{i,j}
]
\end{document}
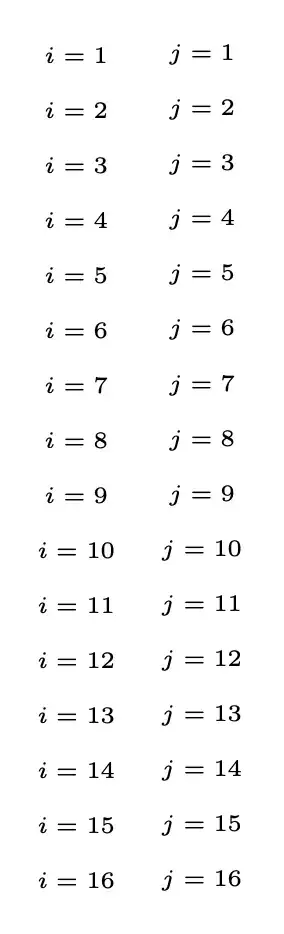
You might enjoy studying the following simpler code.
\documentclass[11pt]{article}
\usepackage{tikz}
\usetikzlibrary{matrix}
\NewDocumentCommand{\tinybox}{m}{\mbox{\tiny#1}}
\ExplSyntaxOn
\NewDocumentCommand{\indexprod}{ O{16} m } % indices
{
% the indices
\seq_set_from_clist:Nn \l_tmpa_seq { #2 }
\seq_set_map:NNn \l_tmpb_seq \l_tmpa_seq { \tinybox{$##1=\int_eval:n { \l_tmpa_int }$} }
\tl_clear:N \l_tmpa_tl
\int_zero:N \l_tmpa_int
\prg_replicate:nn { #1 }
{
\int_incr:N \l_tmpa_int
\tl_set:Nx \l_tmpb_tl { \seq_use:Nn \l_tmpb_seq { & } }
\tl_put_right:Nx \l_tmpa_tl { \l_tmpb_tl \exp_not:N \ }
}
\begin{tikzpicture}[baseline={([yshift=-0ex]current~bounding~box.center)}]
\matrix(m) [
matrix~of~nodes,
ampersand~replacement=&,
column~sep=1ex,
nodes~in~empty~cells,
nodes={
shape=rectangle,
minimum~height=3ex,
anchor=center
},
]{
\tl_use:N \l_tmpa_tl
};
\end{tikzpicture}
}
\ExplSyntaxOff
\begin{document}
[
\indexprod{i,j}\qquad
\indexprod[5]{i,j,k}
]
\end{document}
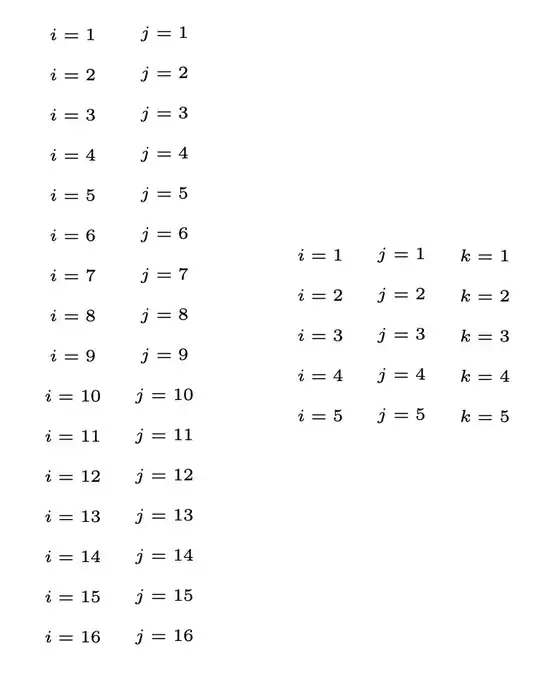
Some comments about the above code. If we \seq_show:N \l_tmpa_seq and \seq_show:N \l_tmpb_seq after they're set we get
The sequence \l_tmpa_seq contains the items (without outer braces):
> {i}
> {j}.
The sequence \l_tmpb_seq contains the items (without outer braces):
> {\tinybox {$i=\int_eval:n {\l_tmpa_int }$}}
> {\tinybox {$j=\int_eval:n {\l_tmpa_int }$}}.
Now add \tl_show:N \l_tmpb_tl and \tl_show:N \l_tmpa_tl after they're set in the \prg_replicate:nn loop: at the first iteration we get
> \l_tmpb_tl=\tinybox {$i=\int_eval:n {\l_tmpa_int }$}\&\tinybox
{$j=\int_eval:n {\l_tmpa_int }$}.
> \l_tmpa_tl=\tinybox {$i=1$}&\tinybox {$j=1$}\.
This uses the fact that the items in the sequence are returned with \exp_not:n around them, so \tl_set:Nx just arrives at the “surface” token list; but after \tl_put_right:Nx the items are fully expanded. In this case I exploit that the items in \l_tmpa_seq are “expansion safe”. Other use cases might need other cares.
Safer version
\documentclass[11pt]{article}
\usepackage{tikz}
\usetikzlibrary{matrix}
\NewDocumentCommand{\tinybox}{m}{\mbox{\tiny#1}}
\NewDocumentCommand{\tbinnermatrix}{m}{%
\begin{tikzpicture}[baseline={([yshift=-0ex]current bounding box.center)}]
\matrix(m) [
matrix of nodes,
ampersand replacement=&,
column sep=1ex,
nodes in empty cells,
nodes={
shape=rectangle,
minimum height=3ex,
anchor=center
},
]{ #1 };
\end{tikzpicture}%
}
\ExplSyntaxOn
\NewDocumentCommand{\indexprod}{ O{16} m } % indices
{
\tedblack_indexprod:nn { #1 } { #2 }
}
\cs_generate_variant:Nn \cs_set:Nn { NV }
\cs_set_eq:NN \tedblack_innermatrix:n \tbinnermatrix
\cs_generate_variant:Nn \tedblack_mymatrix:n { V }
\cs_new_protected:Nn \tedblack_indexprod:nn
{
% the indices
\seq_set_from_clist:Nn \l_tmpa_seq { #2 }
\seq_set_map:NNn \l_tmpa_seq \l_tmpa_seq { \tinybox{$\exp_not:n { ##1 }=####1$} }
\tl_set:Nx \l_tmpa_tl { \seq_use:Nn \l_tmpa_seq { & } }
\cs_set:NV __tedblack_temp:n \l_tmpa_tl
\tl_clear:N \l_tmpa_tl
\int_step_inline:nn { #1 }
{
\tl_put_right:Nx \l_tmpa_tl { __tedblack_temp:n { ##1 } \exp_not:N \ }
}
\tedblack_innermatrix:V \l_tmpa_tl
}
\ExplSyntaxOff
\begin{document}
[
\indexprod{i,j}\qquad
\indexprod[5]{i,j,\mathbf{k}}
]
\end{document}
This not only shows that “risky” commands such as \mathbf are safe in the argument to \indexprod, but also shows better programming style where there is a distinction between user level commands and internal functions.
The “matrix building” command is taken outside \ExplSyntaxOn, which is always best when TikZ is involved. An internal version is defined later, with the possibility to define a variant thereof.
A “local” function is defined so it can be used to substitute the current value in the \int_step_inline:nn loop.
\documentclass[11pt]{article}
\usepackage{tikz}
\usetikzlibrary{matrix}
\NewDocumentCommand{\tinybox}{m}{\mbox{\tiny#1}}
\NewDocumentCommand{\tbinnermatrix}{m}{%
\begin{tikzpicture}[baseline={([yshift=-0ex]current bounding box.center)}]
\matrix(m) [
matrix of nodes,
ampersand replacement=&,
column sep=1ex,
nodes in empty cells,
nodes={
shape=rectangle,
minimum height=3ex,
anchor=center
},
]{ #1 };
\end{tikzpicture}%
}
\ExplSyntaxOn
\NewDocumentCommand{\indexprod}{ O{16} m } % indices
{
\tedblack_indexprod:nn { #1 } { #2 }
}
\cs_generate_variant:Nn \cs_set:Nn { NV }
\cs_set_eq:NN \tedblack_innermatrix:n \tbinnermatrix
\cs_generate_variant:Nn \tedblack_innermatrix:n { V }
\cs_new_protected:Nn \tedblack_indexprod:nn
{
% the indices
\seq_set_from_clist:Nn \l_tmpa_seq { #2 }
\seq_set_map:NNn \l_tmpa_seq \l_tmpa_seq { \tinybox{$\exp_not:n { ##1 }=####1$} }
\tl_set:Nx \l_tmpa_tl { \seq_use:Nn \l_tmpa_seq { & } }
\cs_set:NV __tedblack_temp:n \l_tmpa_tl
\tl_clear:N \l_tmpa_tl
\int_step_inline:nn { #1 }
{
\tl_put_right:Nx \l_tmpa_tl { __tedblack_temp:n { ##1 } \exp_not:N \ }
}
\tedblack_innermatrix:V \l_tmpa_tl
}
\ExplSyntaxOff
\begin{document}
[
\indexprod{i,j}\qquad
\indexprod[5]{i,j,\mathbf{k}}
]
\end{document}
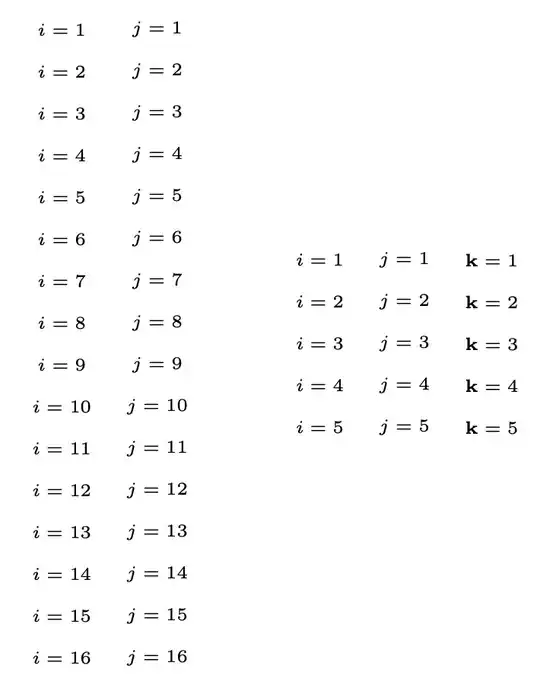
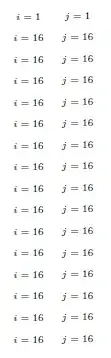
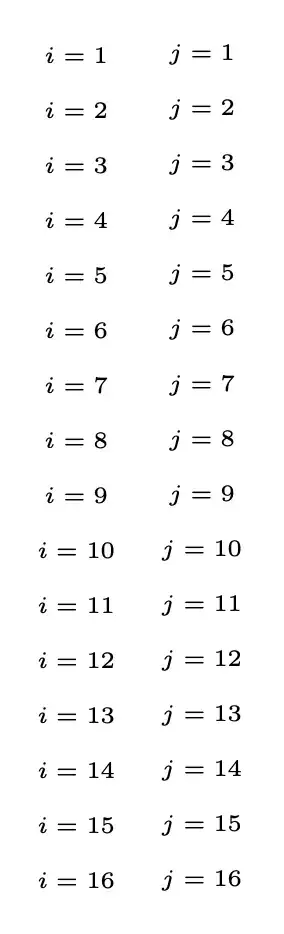
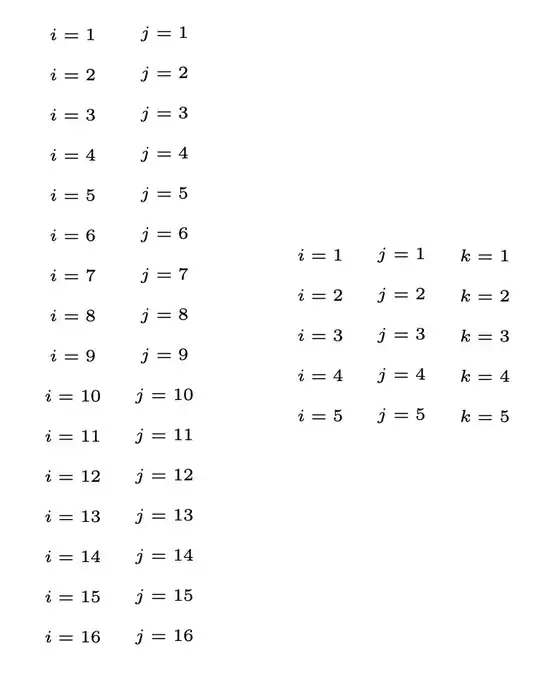
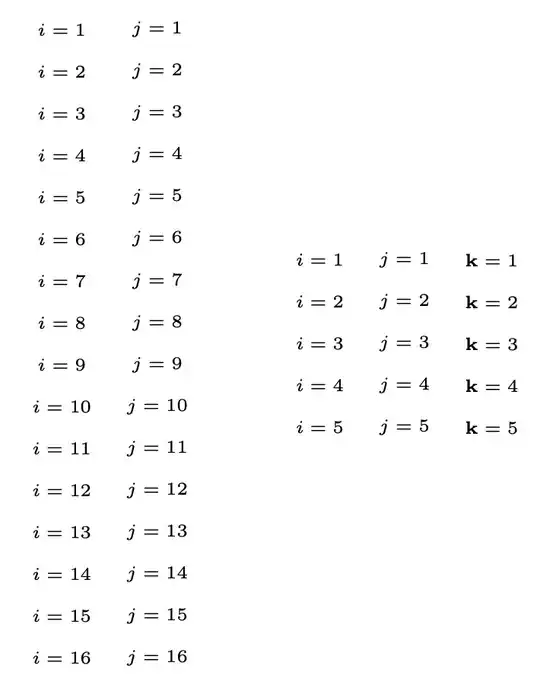
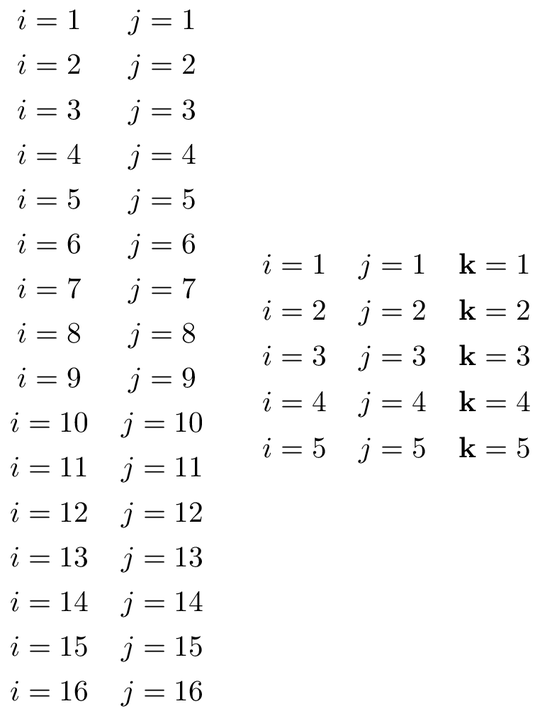
\tl_put_right:Nnis putting variable references in the sequence so when you use the sequence you just get the same value each time, you wantNxto make a sequence of values – David Carlisle Sep 02 '23 at 22:02