Parallel lines on a grid and circle best practices?

Question

I am a TeX/LaTeX noob, but I am learning rapidly. I am about to attempt to draw the following figure using LaTeX/TeX/TikZ I already have a, (I think) good working knowledge of how to draw circles, braces, lines, segments, and nodes, etc.

The last time I drew one though, I noticed that I spent a lot of time fine tuning parameters, making sure that lines intersected circles at the proper points, making sure lines were parallel, etc.

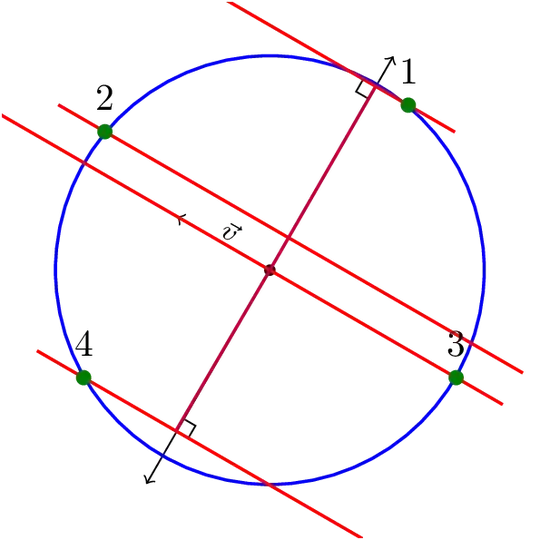
I need to draw the following figure, so I wanted first inquire if there is a fast/easy way, or anything I should keep in mind, when creating parallel lines (the red ones), as per the following figure:

The main time sinks I foresee are going to be the following:

1. Making sure the length of the purple lines are exactly correct, so as not to overshoot the red ones.

2. Making sure the red lines are all parallel to each other.

3. Making sure than I can draw nodes/dots where lines intersect each other and/or the circle.

Is there any particular way(s) that is recommended to make sure that the above points do not waste too much time? I would appreciate any advice/examples.

Thanks!

P.S. I am making good use of TikZ as well.

EDIT:

I am including a minimal example of my 'skill' set. As you can see, I painstakingly usually just have to fine tune co-ordinates, for where things intersect, etc. I also do not know how to not-waste-time if I wanted to make parallel lines, as shown in the red lines above. Here is my example code:

\documentclass[journal]{IEEEtran}
\usepackage{graphicx}
\usepackage{float}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{tikz}
\usetikzlibrary{matrix}
\usetikzlibrary{decorations.pathreplacing}
\usepackage{xspace} 
\usepackage{float}
\usepackage{capt-of}
\usepackage{cases}



\begin{document}

\newcommand{\var}{1.5}

\begin{tikzpicture}
%\begin{tikzpicture}

    \draw [help lines] (-4,-4) grid (4,4);

    % Draw the axes
    \draw [->,black, ] (-4,0) -- (4,0) ;
    \draw [->,black] (0,-4) -- (0,4) ;

    % Draw the circle
    \path [draw, ultra thick,  black] (0,0) circle (3);

    %Radial Lines    
    \draw[black](0:0)--(45:3);
    \draw[black](0:0)--(135:3);
    \draw[black](0:0)--(225:3);
    \draw[black](0:0)--(315:3);        

    %Wavefront normal
    \draw[blue](0:0)--(60:3);
    \draw[blue](0:0)--(240:3);

    \draw[blue](0,1) arc (90:60:1);
    \draw[blue] (0,0.95)arc(90:60:0.95);
    \node[] at (75:1.2)  {$\alpha$};

    \draw[blue] (0.7,1.2)arc(90:30:0.37);
    %\node[] at (50:2) {$\frac{pi}{4}-\alpha$};
    \draw[-latex](1.5,3)node[right]{$\frac{\pi}{4}-\alpha$}
        to[out=180,in=90] (50:1.5);

    %Points
    \path[fill, black](45:3) circle(0.1);
    \node[] at (45:3.3){1};
    \path[fill, black](135:3) circle(0.1);
    \node[] at (133:3.3){4};
    \path[fill,black](225:3) circle(0.1);
    \node[] at (225:3.3){3};
    \path[fill, black](315:3) circle(0.1);
    \node[] at (313:3.3){2};

    %Wavefronts
    \draw[blue, ultra thick](-.5,3.6347)--(3.5,1.3252);
    \draw[blue, ultra thick](-2.5,2.34)--(3.5,-1.1242);
    \draw[blue, ultra thick](-3.2,0.9509)--(2.8,-2.5132);
    \draw[blue, ultra thick](-3.2,-1.4985)--(0.2,-3.4615);

    %Right angle signs
    \draw[red](60:2.8)--(62:2.8)--(62:2.9);
    \draw[red](60:.68)--(68:.69)--(67:.79);




    % Done
\end{tikzpicture}


\end{document}

The above code is now giving me this:

Answer 1

The first TikZ picture shows a rather sloppy idea to draw the parallel lines. The second example shows a more automatic way of drawing secants (one could have used the \angle value directly but I want do show how I’d do it, if the direction of the vector is not known to the user.

The second example also shows that calc’s ($(<p1>)!(<p3>)!(<p2>)$) isn’t very exact for close (<p1>) and (<p2>). Of course, there isn’t even a line when <p1> = <p2>.

The intersections library might be more precise in finding points where the orthogonal line to the vector and the secants intersect.

Code

\documentclass[tikz,convert=false]{standalone}
\usetikzlibrary{calc,through}
\tikzset{
  m*/.style args={#1:#2}{
    insert path={node [fill=green!50!black, outer sep=+0pt, shape=circle, inner sep=0pt, minimum size=+4pt,#1,label={#2}] {}}
  },
  m/.style={insert path={coordinate (#1)}},
  parLines/.style={draw=red,,shorten <=+-.5cm,shorten >=-.5cm},
  vertLines/.style={draw=purple,shorten >=.5\pgflinewidth},
  @splitLine/.code args={#1 -- #2}{\def\tikztotargetA{#1}\def\tikztotargetB{#2}},
  vert on/.style={
    to path={
      [@splitLine/.expanded={\tikztotarget}]
      -- ($(\tikztotargetA)!(\tikztostart)!(\tikztotargetB)$) node[right angle node,rotate=90*#1] {}\tikztonodes
    }
  },
  vert on/.default=0,
  right angle node/.style={
    at end,sloped,above,allow upside down,
    anchor=south east,
    shape=rectangle,
    inner sep=0pt,
    minimum size=3pt,
    append after command={
      \pgfextra\pgfinterruptpath\draw[right angle node path] (\tikzlastnode.south west) -- (\tikzlastnode.north west) -- (\tikzlastnode.north east);\endpgfinterruptpath\endpgfextra
    }
  },
  right angle node path/.style={draw,thin,black,-,shorten >=.4pt},
  secant/.style={
    to path={
      let \p{@dir}=(\tikztotarget), \n{@dir}={atan2(\x{@dir},\y{@dir})} in
      (node cs: name=\tikztostart, anchor=#1) [m*={name=m#1}:#1] -- (node cs: name=\tikztostart, anchor={2*(\n{@dir}-90)-#1}) [m=m#1'] \tikztonodes
    }
  }
}
\begin{document}
\begin{tikzpicture}[thick]
\clip (-2.5,-2.5) rectangle (2.5,2.5);
\draw[thin, ->] (0,0) [m*={black,minimum size=+3pt,name=O}:] -- node [sloped,above,inner sep=+1pt,font=\scriptsize] {$\vec v$} ++(150:1) coordinate (d);

\draw[thin, ->] (0,0) -- ([rotate=90]d)  [shorten >=-1.3cm];
\draw[thin, ->] (0,0) -- ([rotate=-90]d) [shorten >=-1.3cm];

\node [draw=blue, circle through={(2,0)}] (c) {};

\draw[parLines] (c.50)  [m*={name=m1}:1] -- ++([scale=2] d)    [m=m1'];
\draw[parLines] (c.140) [m*={name=m2}:2] -- ++([scale=-4] d)   [m=m2'];
\draw[parLines] (c.-30) [m*={name=m3}:3] -- ++([scale=4.5] d)  [m=m3'];
\draw[parLines] (c.210) [m*={name=m4}:4] -- ++([scale=-2.5] d) [m=m4'];

\draw[vertLines] (c.center) to[vert on] (m1 -- m1');
\draw[vertLines] (c.center) to[vert on] (m4' -- m4);
\end{tikzpicture}

\foreach \angle in {0,10,...,359}{% Careful, 36 pages!
\begin{tikzpicture}[thick]
\clip (-2.5,-2.5) rectangle (2.5,2.5);
\draw[thin, ->] (0,0) [m*={black,minimum size=+3pt,name=O}:] -- node [sloped,above,inner sep=+1pt,font=\scriptsize] {$\vec v$} ++(\angle:1) coordinate (d);

\draw[thin, ->] (0,0) -- ([rotate=90]d)  [shorten >=-1.3cm];
\draw[thin, ->] (0,0) -- ([rotate=-90]d) [shorten >=-1.3cm];

\node [draw=blue, circle through={(2,0)}] (c) {};

\draw[parLines] (c) to[secant=30]  (d);
\draw[parLines] (c) to[secant=140] (d);
\draw[parLines] (c) to[secant=-30] (d);
\draw[parLines] (c) to[secant=210] (d);


\draw[vertLines] (c.center) to[vert on] (m30 -- m30');
\draw[vertLines] (c.center) to[vert on] (m210' -- m210);
\end{tikzpicture}%
}
\end{document}

Output

Answer 2

Solution with tkz-euclide, we get the parallel lines with

  \tkzDefLine[parallel=through B](a,A)     \tkzGetPoint{b} 

The new line goes through B and it's a parallel to Aa, we get a point b of this line.

 \documentclass{article}
 \usepackage{tkz-euclide}
 \usetkzobj{all}

 \begin{document}
 \begin{tikzpicture}
    % init the picture
    \tkzInit[xmin=-5,xmax=5,ymin=-5,ymax=5]
    \tkzGrid \tkzClip
    % definition of points  
    \tkzDefPoint(45:3){A}  
    % it was possible to use random points something like
    % \tkzGetRandPointOn[circle = center O radius 3 cm]{A}  
    \tkzDefPoint(0,0){O}
    \tkzDefPoint(135:3){B}  
    \tkzDefPoint(225:3){C}  
    \tkzDefPoint(315:3){D}  
     \tkzDefPoint(60:3){M} 
     \tkzDefPoint(240:3){N} 
    \tkzDefPoint(-1,4){a} 
    % definition of parallel lines
    \tkzDefLine[parallel=through B](a,A)     \tkzGetPoint{b}    
    \tkzDefLine[parallel=through C](a,A)     \tkzGetPoint{c}    
    \tkzDefLine[parallel=through D](a,A)     \tkzGetPoint{d}
    % orthogonal projection of O on the first line  
    \tkzDefPointBy[projection=onto A--a](O)  \tkzGetPoint{H}  
    % we can avoid the next line and use tkzInterLL 
    \tkzDefPointBy[projection=onto C--c](O)  \tkzGetPoint{K}     
    \tkzInterLL(K,H)(b,B)                    \tkzGetPoint{L}  
    % now we can draw         
    \tkzDrawCircle[R,thick](O,3 cm)
    \tkzDrawLines[add=1 and 1,color=blue](a,A B,b C,c)
    \tkzDrawLine[add=2 and 1,color=blue](D,d)   
     \tkzDrawSegments(A,C B,D)
    \tkzDrawLine[add=2 and 1,color=red](O,H)
     % mark right angles    
    \tkzMarkRightAngles[fill=lightgray](a,H,O C,K,O B,L,O)
     % draw points
    \tkzDrawPoints(A,B,C,D,O)
    % mark angles
     \tkzMarkAngle[mark= ,arc=ll,size=1 cm,mkcolor=blue](H,O,B)
     \tkzLabelAngle[pos=1.25](H,O,B){$\alpha$}
     \tkzMarkAngle[mark= ,arc=l,size=2.25 cm,mkcolor=blue](A,O,H)
     \tkzLabelAngle[pos=2.5,below=10pt](A,O,H){$\frac{\pi}{4}-\alpha$}
    % label points
     \tkzLabelPoint[right](A){$1$} \tkzLabelPoint[right](D){$4$}
     \tkzLabelPoint[above](B){$2$}  \tkzLabelPoint[below](C){$3$}
 \end{tikzpicture}
 \end{document}   

Answer 3

Using PSTricks can be regarded as the best practice. The following code should be clear enough so the remaining is intentionally left as your homework.

\documentclass[pstricks,border=12pt]{standalone}
\usepackage{pst-eucl}
\psset{PointName=none,PointSymbol=none}

\begin{document}
\begin{pspicture}[showgrid](-3,-3)(3,3)
    \pnodes{O}(0,0)(2,0)
    \pstCircleOA{O0}{O1}
    \pnodes{P}(-3,3)(3,1)
    \pcline[nodesepA=1.5,nodesepB=.5](P0)(P1)
    \pstInterLC[PointSymbolB=*]{P0}{P1}{O0}{O1}{I0}{I2}
    \pstProjection{P0}{P1}{O0}
    \psline(O0)(O0')
    \pstRightAngle[RightAngleSize=0.15]{P0}{O0'}{O0}
    \pstTranslation[DistCoef=0.5]{O0'}{O0}{P0,P1}
    \pcline[nodesepA=1.5,nodesepB=.5](P0')(P1')
    \pstInterLC[PointSymbolA=*]{P0'}{P1'}{O0}{O1}{I0'}{I1'}
\end{pspicture}
\end{document}