Drawing the three perpendicular bisectors of the sides of a triangle

Question

(1). L, M and N must be the mid-points of the sides AB, AC and BC respectively.

(2). LX, MY and NZ must be the perpendiculars.

(3). Note that LX and NZ must intersect at point P, and MY must terminate before passing through the point P.

 \documentclass[11pt,a4paper]{article}
 \usepackage{blindtext}
 \usepackage{tikz}
 \usepackage{tkz-euclide}
 \usetkzobj{all}
 \usepackage{color}

 \begin{document}
 \normalsize{\textbf{Theorem 1.25.} \textit{The three perpendicular bisectors of the sides of a triangle meet in a point which is equally distant from the vertices.}}
 \begin{center}
\begin{tikzpicture}
\clip
(-1,-3) rectangle (13,8);
\tkzDefPoint(0,0){A}
\tkzDefPoint(12,0){B}
\tkzLabelPoints[below](A)
\tkzLabelPoints[below](B)
\tkzDrawSegment(A,B)
\tkzDefPoint(4,7){C}
\tkzLabelPoints[above](C)
\tkzDrawSegment(A,C)
\tkzDrawSegment(B,C)


\end{tikzpicture}
\end{center}
 \end{document}

Answer 1

To find the midpoints L, M, N:

\tkzDefMidPoint(A,B) \tkzGetPoint{L}

To find auxiliary points X, Y, Z on the bisectors of the line segments:

\tkzDefLine[orthogonal=through L](A,B) \tkzGetPoint{X}

or

\tkzDefLine[mediator](A,B) \tkzGetPoint{X}

To find intersection P of two bisectors AX and BY:

\tkzInterLL(L,X)(M,Y) \tkzGetPoint{P}

 \documentclass[11pt,a4paper]{article}
 \usepackage{blindtext}
 \usepackage{tikz}
 \usepackage{tkz-euclide}
 \usetkzobj{all}
 \usepackage{color}

 \begin{document}
 \normalsize{\textbf{Theorem 1.25.} \textit{The three perpendicular bisectors of the sides of a triangle meet in a point which is equally distant from the vertices.}}
 \begin{center}
\begin{tikzpicture}
\clip
(-1,-3) rectangle (13,8);
\tkzDefPoint(0,0){A}
\tkzDefPoint(12,0){B}
\tkzDefPoint(4,7){C}

\tkzDrawSegment(A,B)
\tkzDrawSegment(B,C)
\tkzDrawSegment(C,A)

\tkzDefMidPoint(A,B) \tkzGetPoint{L}
\tkzDefLine[orthogonal=through L](A,B) \tkzGetPoint{X}

\tkzDefMidPoint(B,C) \tkzGetPoint{M}
\tkzDefLine[orthogonal=through M](B,C) \tkzGetPoint{Y}

\tkzDefMidPoint(C,A) \tkzGetPoint{N}

\tkzInterLL(L,X)(M,Y) \tkzGetPoint{P}

\tkzDrawLines(L,X M,Y)
\tkzDrawSegment(N,P)
\tkzMarkRightAngle(A,L,X)
\tkzMarkRightAngle(B,M,Y)
\tkzMarkRightAngle(C,N,P)

\tkzLabelPoints(B,L)
\tkzLabelPoints[below left](A)
\tkzLabelPoints[above](C,M)
\tkzLabelPoints[above left](N)
\tkzLabelPoints[below right](P)

\end{tikzpicture}
\end{center}
 \end{document}

Answer 2

With MetaPost, as an complement for whom it may interest. With help from the MetaPost manual and André Heck's MetaPost tutorial for the macros mark_right_angle, draw_mark and tick.

To find the midpoints:

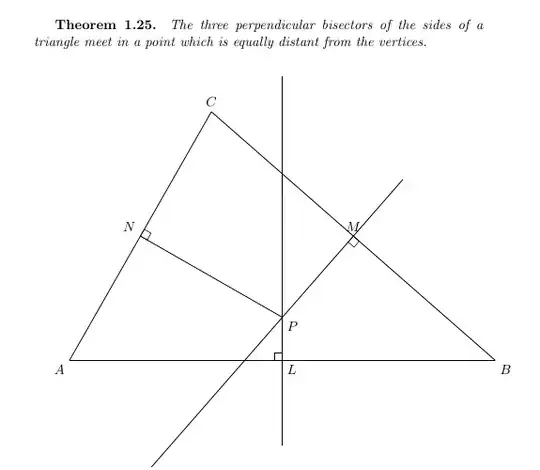
L = .5[A, B]; M = .5[A, C]; N = .5[B, C];

The intersection point is found with implicit equations, as often with MetaPost:

P = whatever[L, L + (B-A) rotated 90] = whatever[N, N + (C-B) rotated 90];

X, Y and Z are built with help of midpoints and numeric parameters over and under (for their positions relatively to P).

X = P + over*unitvector(P-L); 
Y = P - under*unitvector(P-M); 
Z = P + over*unitvector(P-N);

The whole code:

\documentclass{scrartcl}
\usepackage{luamplib}
    \mplibtextextlabel{enable}
\begin{document}
\begin{mplibcode}

vardef mark_right_angle (expr common, endofa, endofb, size) = % right angle mark
    save tn ; tn := turningnumber(common -- endofa -- endofb -- cycle) ;
    draw ((1, 0) -- (1, 1) -- (0, 1))
        zscaled (size*unitvector((1+tn)*endofa + (1-tn)*endofb - 2*common))
        shifted common;
enddef ;

vardef draw_mark(expr p, m, size) = % One mark upon a segment
    save t, dm; pair dm;
    t = arctime m of p;
    dm = size*unitvector(direction t of p rotated 90);
    draw (-.5dm .. .5dm) shifted (point t of p); 
enddef;


vardef tick(expr p, n, size) = % Several marks upon a segment
    save midpnt; midpnt = 0.5*arclength(p);
    for i = -(n-1)/2 upto (n-1)/2:
        draw_mark(p, midpnt+0.6size*i/2, size); 
    endfor;
enddef;

u := 1cm; over := u; under := 0.75u;
pair A, B, C, L, M, N, P, X, Y, Z; path triangle;
A = origin; B = (12u, 0); C = u*(4, 7);
triangle = A -- B -- C -- cycle; 
L = .5[A, B]; M = .5[A, C]; N = .5[B, C];
% Locating the intersection
P = whatever[L, L + (B-A) rotated 90] = whatever[N, N + (C-B) rotated 90];
% Bisectors 
X = P + over*unitvector(P-L); 
Y = P - under*unitvector(P-M); 
Z = P + over*unitvector(P-N);

beginfig(1);
    rsize := 2mm; msize := 3mm;
    draw triangle; draw L -- X; draw M -- Y; draw N -- Z;
    mark_right_angle(L, B, P, rsize); tick(A--L, 2, msize); tick(L--B, 2, msize);
    mark_right_angle(M, C, P, rsize); tick(A--M, 1, msize); tick(C--M, 1, msize); 
    mark_right_angle(N, C, P, rsize); tick(C--N, 3, msize); tick(B--N, 3, msize);
    label.llft("$A$", A); label.bot("$B$", B);
    label.top("$C$", C); label.rt("$P$", P);
    label.llft("$L$", L); label.ulft("$M$", M);
    label.urt("$N$", N); label.top("$X$", X);
    label.bot("$Y$", Y); label.lft("$Z$", Z);
endfig;

\end{mplibcode}
\end{document}

To be processed with LuaLaTeX: