How to create board game search tree?

Question

How can I create a visualization for the search tree in a game where I don't want to see only the nodes, but the board configuration at each step? Any code help for this image for example would be highly appreciated.

[Edit]: unfortunately I don't have much until now: I know how to generate such a matrix, but I do not know how to go about creating the edges and the rest of the matrices, all in one picture.

\begin{figure}
\centering
\begin{tikzpicture}[rotate=270]
\centering
   \draw[-, very thick] (0,0) grid +(3,3);
\draw (0.5, 0.5) node {3};
\draw (0.5, 1.5) node {};
\draw (0.5, 2.5) node {};
\draw (1.5, 0.5) node {5};
\draw (1.5, 1.5) node {};
\draw (1.5, 2.5) node {2};
\draw (2.5, 0.5) node {1};
\draw (2.5, 1.5) node {6};
\draw (2.5, 2.5) node {4};
\end{tikzpicture}
 \caption{Example}
 \label{fig:example}
\end{figure}

Answer 1

You can draw a tree with tikz and insert tables inside the nodes.

\documentclass[border=10pt]{standalone}
\usepackage{tikz}

\begin{document}
\begin{tikzpicture}[
        level distance=25mm,
        level 1/.style={sibling distance=50mm},
        level 2/.style={sibling distance=30mm},
        level 3/.style={sibling distance=30mm},
        every node/.style = {shape=rectangle, align=center}
    ]
    \node{
        $U = 4$\\[1mm]
        \begin{tabular}{|c|c|c|}
            \hline
            6 &   &  \\ \hline
            1 & 5 &  \\ \hline
            4 & 2 & 3\\ \hline
        \end{tabular}\hfill\\[1mm]
        $L = 2$
    } [grow=right]
    child{
        node{
            $U = 4$\\[1mm]
            \begin{tabular}{|c|c|c|}
                \hline
                  &   &  \\ \hline
                1 & 5 & 6\\ \hline
                4 & 2 & 3\\ \hline
            \end{tabular}\hfill\\[1mm]
            $L = 3$
        }
    }
    child{
        node{
            $U = 5$\\[1mm]
            \begin{tabular}{|c|c|c|}
                \hline
                  & 6 &  \\ \hline
                1 & 5 &  \\ \hline
                4 & 2 & 3\\ \hline
            \end{tabular}\hfill\\[1mm]
            $L = 3$
        }
        child{
            node{
                \begin{tabular}{|c|c|c|}
                    \hline
                      &   &  \\ \hline
                    6 & 5 &  \\ \hline
                    4 & 2 & 3\\ \hline
                \end{tabular}\hfill\\[1mm]
                $U = 5$, $L = 3$
            }
        }
        child{
            node{
                \begin{tabular}{|c|c|c|}
                    \hline
                      &   &  \\ \hline
                      & 5 & 6 \\ \hline
                    4 & 2 & 3\\ \hline
                \end{tabular}\hfill\\[1mm]
                $U = 5$, $L = 3$
            }
        }
    };
\end{tikzpicture}
\end{document}

Answer 2

I took the tabular definitions from dexteritas's answer, to avoid having to type everything from the image, added definitions for the matrices omitted from that answer and wrapped the result in a forest environment. The advantage of using Forest is that the tree specification is much more concise and that the format can be automated for greater flexibility and consistency. That is, it means less typing and more maintainable code.

We create U and L as token lists to hold the relevant values. These can then be specified as key-value options in the tree.

\forestset{
  declare toks={U}{},
  declare toks={L}{},
}

We don't need an explicit tabular environment or similar. We can use Forest's align and we'll get a tabular setup. Rather than specifyking all the horizontal rules, we can add the top and bottom ones automatically. We set the direction of growth to 0 (east/right), overriding the default.

\begin{forest}
  for tree={
    grow'=0,
    align=|c|c|c|,
    delay={content/.wrap value=\hline #1\\\hline},
    child anchor=parent,
    l sep'+=20pt,
  },

We add the code to handle the U and L. For terminal nodes, we add these as a label to the right. In other cases, we add it into the tabular using a \multicolumn. This means we don't have to worry about spacing: Forest will figure it out automatically. When we're dealing with terminal nodes, we also add the circle onto the end of the edge drawn from the parent.

  before typesetting nodes={
    where n children=0{
      label/.process={OOw2 {U}{L} {right:{U=#1, L=#2}}},
      edge+={-Circle},
    }{
      content/.process={ OOOw3 {content}{U}{L} {\multicolumn{3}{c}{U=#2}\\#1\multicolumn{3}{c}{L=#3} } },
    },
  }

Now for the tree specification. Here's the root, with values for U and L.

  [6 &   &  \\ \hline 1 & 5 &  \\ \hline 4 & 2 & 3, U=4, L=2

We continue in the same way.

    [& 6 &  \\ \hline 1 & 5 &  \\ \hline 4 & 2 & 3, U=5, L=3
      [&   &  \\ \hline & 5 & 6 \\ \hline 4 & 2 & 3, U=5, L=4
      ]
      [&   &  \\ \hline 6 & 5 &  \\ \hline 4 & 2 & 3, U=5, L=4
      ]
    ]
    [&   &  \\ \hline 1 & 5 & 6\\ \hline 4 & 2 & 3, U=4, L=3
      [&   &  \\ \hline  5 && 6 \\ \hline 4 & 2 & 3, U=4, L=4
      ]
      [&   & 5 \\ \hline && 6 \\ \hline 4 & 2 & 3, U=5, L=4
      ]
    ]
  ]
\end{forest}

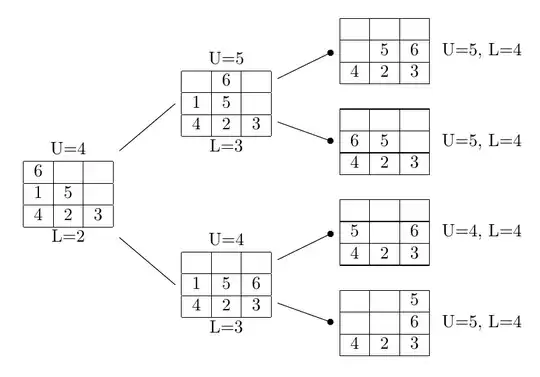
Complete code:

\documentclass[border=10pt]{standalone}
\usepackage{forest}
\usetikzlibrary{arrows.meta}
\begin{document}
\forestset{
  declare toks={U}{},
  declare toks={L}{},
}
\begin{forest}
  for tree={
    grow'=0,
    align=|c|c|c|,
    delay={content/.wrap value=\hline #1\\\hline},
    child anchor=parent,
    l sep'+=20pt,
  },
  before typesetting nodes={
    where n children=0{
      label/.process={OOw2 {U}{L} {right:{U=#1, L=#2}}},
      edge+={-Circle},
    }{
      content/.process={ OOOw3 {content}{U}{L} {\multicolumn{3}{c}{U=#2}\\#1\multicolumn{3}{c}{L=#3} } },
    },
  }
  [6 &   &  \\ \hline 1 & 5 &  \\ \hline 4 & 2 & 3, U=4, L=2
    [& 6 &  \\ \hline 1 & 5 &  \\ \hline 4 & 2 & 3, U=5, L=3
      [&   &  \\ \hline & 5 & 6 \\ \hline 4 & 2 & 3, U=5, L=4
      ]
      [&   &  \\ \hline 6 & 5 &  \\ \hline 4 & 2 & 3, U=5, L=4
      ]
    ]
    [&   &  \\ \hline 1 & 5 & 6\\ \hline 4 & 2 & 3, U=4, L=3
      [&   &  \\ \hline  5 && 6 \\ \hline 4 & 2 & 3, U=4, L=4
      ]
      [&   & 5 \\ \hline && 6 \\ \hline 4 & 2 & 3, U=5, L=4
      ]
    ]
  ]
\end{forest}
\end{document}