I'm struggling to make all the matrices in my equation of same height (vertical alignment). I would appreciate if I could get some suggestions. I tried some solutions here and there but it's looks my question is different.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
\begin{equation} \label{eq:system_dynamics_l}
\begin{bmatrix}
m_1+m_2 & \dfrac{1}{2}m_2 L \\\[4mm\]
\dfrac{1}{2}m_2 L & \dfrac{1}{2}m_2 L^2
\end{bmatrix}
\begin{bmatrix}
\ddot{x} \\\[4mm\] \ddot{\theta}
\end{bmatrix}
+ \begin{bmatrix}
b & 0 \\\[4mm\]
0 & c
\end{bmatrix}\begin{bmatrix}
\dot{x} \\\[4mm\] \dot{\theta}
\end{bmatrix}
+\begin{bmatrix}
k & 0 \\\[4mm\] 0 & m_2g\dfrac{L}{2}
\end{bmatrix}\begin{bmatrix}
x \\\[4mm\] \theta
\end{bmatrix}
=\begin{bmatrix}
0 \\\[4mm\] 0
\end{bmatrix}
\end{equation}
\end{document}


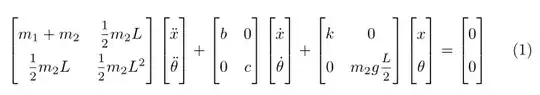
\tfracfor your fractions – Elements In Space Apr 26 '18 at 13:40\dfrac{1}{2}? (just use\frac) – David Carlisle Apr 26 '18 at 13:40