Circles touching path

Question

That is what I have so far:

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\usetikzlibrary{intersections,decorations}

\begin{tikzpicture}[thick,
    dot/.style = {
        draw,
        fill = black,
        circle,
        inner sep = 0pt,
        minimum size = 2pt
}]

    \draw[smooth cycle, tension=0.6] plot coordinates{(-1,-.4) (1.1,-.6) (.9,.5) (-1.1,.5)} node at (1,.6) {$\Omega$};
    \draw[blue] (-1.1,.5) .. controls (-.5,-.2) and (.5,0) .. coordinate[dot,pos=0.3,black] (A) coordinate[dot,pos=0.5,black] (B) coordinate[dot,pos=0.7,black] (C) coordinate[pos=0.92,black] (D) (1.1,-.6);
    \draw[gray] (A) circle (.3);
    \draw[gray] (B) circle (.375) node[black,anchor=north] {$x_0$};
    \node[anchor=south,gray] at ([yshift=10]B) {$\gamma(\bar{D})$};
    \draw[gray] (C) circle (.3);
    \node[blue,anchor=south west] at (D) {$S$};

\end{tikzpicture}

\end{document}

which looks like

Now, I want to add two dashed lines at each side of S going from the beginning and end of S touching the circles exactly such that each circle stays within.

Something like:

There is a \begin{document} missing, graphicblue is not a color defined in your MWE and you might want to reword the question such that it becomes clearer. — , Nov 27 '18 at 14:49

score 3 · Answer 1 · 2018-11-27T17:09:42.813

UPDATE: Using tangents, see e.g. this nice answer.

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{calc}
\begin{document}

\begin{tikzpicture}[thick,
    dot/.style = {
        draw,
        fill = black,
        circle,
        inner sep = 0pt,
        minimum size = 2pt
}]

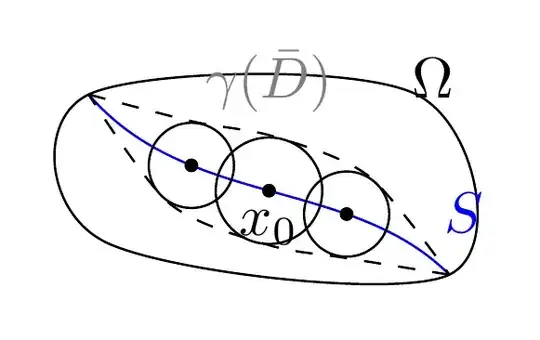
    \draw[smooth cycle, tension=0.6] plot coordinates{(-1,-.4) (1.1,-.6) (.9,.5) (-1.1,.5)} node at (1,.6) {$\Omega$};
    \draw[blue] (-1.1,.5) coordinate(start) .. controls (-.5,-.2) and (.5,0) ..
    coordinate[dot,pos=0.3,black] (A) coordinate[dot,pos=0.5,black] (B)
    node[black,anchor=north] {$x_0$} coordinate[dot,pos=0.7,black] (C) coordinate[pos=0.92,black] (D) (1.1,-.6)
    coordinate(end);
    % see https://tex.stackexchange.com/a/76226/121799
    \pgfmathsetmacro{\rsmall}{0.6}
    \pgfmathsetmacro{\rbig}{0.75}
    \node [draw=gray,circle,minimum size=\rsmall*1cm] (cA) at (A){};
    \node [draw=gray,circle,minimum size=\rbig*1cm] (cB) at (B){};
    \node[anchor=south,gray] at ([yshift=10]B) {$\gamma(\bar{D})$};
    \node [draw=gray,circle,minimum size=\rsmall*1cm] (cC) at (C){};
    \node[blue,anchor=south west] at (D) {$S$};
    \begin{scope}[overlay] % see https://tex.stackexchange.com/a/76226/121799
    \coordinate (cAB) at (barycentric cs:B=-\rsmall,A=\rbig);
    \coordinate (cCB) at (barycentric cs:B=-\rsmall,C=\rbig);
    \end{scope}
    \foreach \Y in {1,2}
    {\foreach \X in {A,C}
    {\path (tangent cs:node=c\X,point={(c\X B)},solution=\Y) coordinate(pB\X-\Y)
    (tangent cs:node=cB,point={(c\X B)},solution=\Y) coordinate(p\X B-\Y);}
    \path (tangent cs:node=cA,point={(start)},solution=\Y) coordinate(pstartA-\Y)
    (tangent cs:node=cC,point={(end)},solution=\Y) coordinate(pendC-\Y); }  
    \draw[red,dashed] plot[smooth] coordinates {(start) (pstartA-2) (pBA-2) (pAB-2) (pCB-1)  (pBC-1)
    (pendC-1) (end)};
    \draw[red,dashed] plot[smooth] coordinates {(start) (pstartA-1) (pBA-1) (pAB-1) (pCB-2)  (pBC-2)
    (pendC-2) (end)};
\end{tikzpicture}
\end{document}

OLDER ANSWER: You started drawing this with Bezier curves (which I may not necessarily have done), so perhaps the best way is to continue this strategy. Yet I think it helps to make the circles nodes such that you can easily access the points on their peripheries.

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}

\begin{tikzpicture}[thick,
    dot/.style = {
        draw,
        fill = black,
        circle,
        inner sep = 0pt,
        minimum size = 2pt
}]

    \draw[smooth cycle, tension=0.6] plot coordinates{(-1,-.4) (1.1,-.6) (.9,.5) (-1.1,.5)} node at (1,.6) {$\Omega$};
    \draw[blue] (-1.1,.5) .. controls (-.5,-.2) and (.5,0) ..
    coordinate[dot,pos=0.3,black] (A) coordinate[dot,pos=0.5,black] (B)
    node[black,anchor=north] {$x_0$} coordinate[dot,pos=0.7,black] (C) coordinate[pos=0.92,black] (D) (1.1,-.6);
    \node [draw=gray,circle,minimum size=0.6cm] (cA) at (A){};
    \node [draw=gray,circle,minimum size=0.75cm] (cB) at (B){};
    \node[anchor=south,gray] at ([yshift=10]B) {$\gamma(\bar{D})$};
    \node [draw=gray,circle,minimum size=0.6cm] (cC) at (C){};
    \node[blue,anchor=south west] at (D) {$S$};
    \draw[red,dashed] (-1.1,0.5) to[out=-20,in=190] (cA.110)
    to[out=10,in=170] (cB.90) to[out=-10,in=170] (cC.80) to[out=-10,in=150] (1.1,-.6); 
    \draw[red,dashed] (-1.1,0.5) to[out=-50,in=150] (cA.250)
    to[out=-20,in=180] (cB.270) to[out=00,in=190] (cC.280) to[out=10,in=180] (1.1,-.6); 
\end{tikzpicture}
\end{document}

score 1 · Answer 2 · answered Nov 27 '18 at 18:03

An empirical solution:

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\begin{tikzpicture}[thin,
    dot/.style = {
        draw,
        fill = black,
        circle,
        inner sep = 0pt,
        minimum size = 2pt
}]

    \draw[smooth cycle, tension=0.6] plot coordinates{(-1,-.4) (1.1,-.6) (.9,.5) (-1.1,.5)} node at (1,.6) {$\Omega$};
    \draw[blue] (-1.1,.5)coordinate(s1) .. controls (-.5,-.2) and (.5,0) .. coordinate[dot,pos=0.3,black] (A) coordinate[dot,pos=0.5,black] (B) node[black,below]{$x_0$} coordinate[dot,pos=0.7,black] (C) coordinate[pos=0.92,black] (D) (1.1,-.6)coordinate(s2);
    \draw (A) node[draw,minimum size=0.52cm,circle] (C1){};
    \draw (B) node[draw,minimum size=0.65cm,circle] (C2){};
    \draw (C) node[draw,minimum size=0.52cm,circle] (C3){};
    \node[blue,anchor=south west] at (D) {$S$};
    \node[anchor=south,gray] at ([yshift=10]B) {$\gamma(\bar{D})$};
    \draw[dashed,smooth, tension=0.5] plot coordinates{(s1) (C1.87)  (C2.85)  (C3.60) (s2)};
    \draw[dashed,smooth, tension=0.5] plot coordinates{(s2) (C3.267) (C2.270) (C1.240) (s1)};    
\end{tikzpicture}
\end{document}

Circles touching path

2 Answers2