Drawing a function without knowing its definition

Question

I don't know TikZ in depth so I barely can play with it. The following is a transfer characteristic of an inverter gate. I have researched on the Internet to find the function's explicit definition without success.

I am trying to draw the curve, without knowing the definition. Yet there is one requirement: the slope at two points of the curve is −1.

I would be so happy of any help.

You can draw a set of connected curves. With in and out in TikZ, the slope = -1 is easy to achieve. — , Feb 19 '19 at 06:46
Can you refer me examples of how it's used? It is foreign to me. — billyandriam, Feb 19 '19 at 06:59
@JouleV On this handout I found a way to draw a function by specifying discrete points and let PGF/Tikz draw the rest. Yet, I don't know in and out. Coud you please help me on this? Thanks in advance. — billyandriam, Feb 19 '19 at 07:37
do you have any more information about the function? this would probably help others in answering your question, i.e. finding the composite curve equation. I am far from being an expert, but I believe, without the equation, you might be better off drawing the curve in e.g. inkscape and then including it in your LaTeX document. Do you have any code to show that shows what you have tried, yet? — thymaro, Feb 19 '19 at 07:38
@thymaro The picture I included above was obtained from the presentation slides in the university course I attend. So, unfortunately, I have no composite curve equation. Even if it is possible for me to use this figure right away in the reports which I have to write, I prefer to make a proper drawing of the function with PGF/Tikz because in my litle experience, dealing with floats and images was no fun. — billyandriam, Feb 19 '19 at 07:43
well, the document you link to has an example at the end of chapter 2 with which you can start playing, changing numbers and see what it does. you will probably get closer to what you want and might run against a hard wall at some point. That is the moment when you can go back to tex.se and ask specific questions. Questions about specific problems tend to produce answers much faster than questions of this type here ;) — thymaro, Feb 19 '19 at 07:45
oh ok, then the presenter should have the equation, I hope. For general information on how to use tikz, I recommend youtube tutorials and/or http://www.texample.net/tikz/examples/ — thymaro, Feb 19 '19 at 07:47
learning TikZ takes some time, but learning the basics is definitely worth it. It will let you ask better questions, i.e. questions that will find an answer ;) — thymaro, Feb 19 '19 at 07:49
@JPi I think it fits more as a sigmoid function. I am curently working on Overleaf and modify the code I found here. — billyandriam, Feb 19 '19 at 08:29
IIRC, the process is inherently statistical. As you raise the voltage, more electrons will have enough energy to jump the gap. Assuming a normal distribution of energy levels, the total current would be a cumulative normal, which alas does not have a simple formula. However, the slope does. — John Kormylo, Feb 19 '19 at 14:40

score 20 · Accepted Answer · edited Jun 10 '20 at 12:32

To get the exact slope without the definition of the function, you can use to[out=...,in=...] by TikZ. The following diagram may show you all about to:

You want slope of the plot is −1 at some points. You can have it by to[out=135,in=-45] if you are going up, or to[out=-45,in=135] if you are going down. This can be proved by using simple trigonometry.

So your plot can be "encoded" to TikZ as

\documentclass[tikz,margin=3mm]{standalone}
\usepackage{mathptmx}
\begin{document}
\begin{tikzpicture} 
\draw[-latex] (0,0) node[below left] {0}--(0,6) node[left] {$v_O$};
\draw[-latex] (0,0)--(6,0) node[below] {$v_I$};
\draw[dashed] (0,5) node[left] {$V_{OH}$}--(1.5,5)--(1.5,0) node[below] {$V_{IL}$};
\draw[dashed] (0,2.5) node[left] {$V_M$}--(2.5,2.5)--(2.5,0) node[below] {$V_M$};
\draw[dashed] (0,0.5) node[left] {$V_{OL}$}--(5,0.5)--(5,0) node[below] {$V_{OH}$};
\draw (0.5,0) node[below] {$V_{OL}$}--(0.5,.1);
\draw[dashed] (3.5,0) node[below] {$V_{IH}$}--(3.5,1);
\draw[very thick,cyan] (5.65,.45) to[out=180,in=-8] (5,.5) to[out=172,in=-45] (3.5,1) to[out=135,in=-70] (2.5,2.5);
\draw[very thick,cyan] (0,5)--(1.4,5) to[out=0,in=135] (1.6,4.9) to[out=-45,in=110] (2.5,2.5);
\draw (1.1,5.4)--(2.1,4.4);
\draw (1.5,5) node[above right] {Slope $=-1$};
\draw (2.9,1.6)--(3.9,0.6);
\draw (3.5,1) node[above right] {Slope $=-1$};
\draw (0,0)--(4,4);
\node (nd) at (5.3,3.5) {Slope $=$ 1}; % Long live the palindromes!
\draw[-latex] (nd) to[out=180,in=-45] (3.8,3.8);
\end{tikzpicture}
\end{document}

It is not really a replicate of your figure, but I think it is close enough.

Important Note

You can use many other awesome methods to draw such a plot (but I'm afraid making the slope equal to −1 is more difficult). A good summary of such methods can be found in this very nice answer.

+1 for the bece explanation of the to directive. But in the provided snapshot the slope lines (tangents) look rather bad, and even seem to not be real tangents... — Jhor, Feb 20 '19 at 08:20
@Jhor Thanks for the upvote. In fact, the slope lines are the real tangents (otherwise there is a bug in TikZ's to), and we can prove the slopes are equal to 1 as well. It is not really clear because the slope lines are too short, I think. I will possibly improve it now. — , Feb 20 '19 at 08:26
@JouleV In fact, the problem merely comes from the fact that you don't have exactly the proper (radius of) curvature. This is more visible on the upper point, where the derivative seems to be (almost) discontinuous. On an other hand, the curve in the OP crosses the horizontal line at V_{OL}, and you draw it more or less as an asymptot. — Jhor, Feb 20 '19 at 08:45
@Jhor I agree. Of course, without the definition of the curve, it is a bit hard, and it requires a bit guess as well. I have to guess at two points: (1) the sharpness at (V_{IL},V_{OH}) and (2) the angle at (V_M,V_M). My figure is clearly a bit different from the OP's at [V_{IL}, V_{M}]. That is why I said "It is not really a replicate of your figure, but I think it is close enough.". The OP should make a slight change in the code to fit the figure better if necessary. — , Feb 20 '19 at 09:05

score 4 · Answer 2 · answered Feb 20 '19 at 02:07

4

This is more an extended comment. Your function looks like a Gaussian.

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{intersections}
\begin{document}
\begin{tikzpicture}[declare function={mygauss(\x)=4*exp(-\x*\x/2)+0.5;}]
 \draw[thick,stealth-stealth] (0,5.5) |- (5,0);
 \draw[thick,cyan,name path=curve] (0,4.5) -- plot[variable=\x,domain=0:4,smooth]({\x+1},{mygauss(\x)});
 \draw[thick,name path=line] (0,0) -- (4,4);
 \path[name intersections={of=curve and line,by=i2}]
 (1+0.2585,{mygauss(0.2585)}) coordinate (i1)
 (1+2.0518,{mygauss(2.0518)}) coordinate (i3)
 (1+3,{mygauss(3)}) coordinate (i4);
 \draw[dashed] (i1|-0,0) node[below]{$V_{IL}$} -- (i1);
 \draw[dashed] (i2|-0,0) node[below]{$V_{M}$} -- (i2) -- (i2-|0,0) node[left]{$V_{M}$};
 \draw[dashed] (i3|-0,0) node[below]{$V_{IH}$} -- (i3);
 \draw[dashed] (i4|-0,0) node[below]{$V_{OH}$} -- (i4) -- 
 (i4-|0,0) node[left]{$V_{OL}$};
 \foreach \X in {1,3}
 {\draw (i\X) -- ++ (-0.3,0.3) -- ++ (0.6,-0.6);}
\end{tikzpicture}
\end{document}

(I have not seen an example on this site that cannot be fitted by some elementary functions like polynomials, sines, exp, tanh, or Gaussian functions.)

answered Feb 20 '19 at 02:07

Thanks for the comment and the extra explanation! This may get out of the scope of tex.se but I would really love to know how you did the fitting process for a random graph encountered. This is useful. – billyandriam Feb 20 '19 at 02:22
@mandresybilly To me this doesn't look random. If you have seen a sign before, an oscillatory function may remind you of a sine. Likewise, this is rather reminiscent of a Gaussian. (From the description of what it is supposed to describe, I would have expected a tanh shape, though.) Many important processes can be modeled by very simple models, and the solutions of the equations of motion are then elementary functions. – Feb 20 '19 at 02:27
I was thinking of a sigmoid. But your expression 4*exp(-\x*\x/2)+0.5 looks so on point. I would never have found it. How? – billyandriam Feb 20 '19 at 02:33
@mandresybilly I am sorry, if you expect a simple recipe, I can't provide one. It is a little bit like mushroom picking: you identify them on the basis of their characteristics. (BTW, have you ever read how Planck got his famous radiation formula?;-) – Feb 20 '19 at 03:11
I guess it's a matter of practice then! Thank you for the advice! And no, I don't know how Planck got his radiation formula but I definitely will look it up. – billyandriam Feb 20 '19 at 03:18
I believe is is actually a cumulative gaussian (AKA erf), scaled and offset of course. Alas, no simple formula, but some relatively simple approximations. Or you could just copy a table. – John Kormylo Feb 20 '19 at 04:54
@JohnKormylo AFAIK is the derivative of erf a Gaussian, and therefore the slope is symmetric. In other words there should be a point reflection symmetry w.r.t. the point at which the second derivative vanishes. It might be just me, but I fail to see this symmetry in the OP's screen shot. – Feb 20 '19 at 05:07
@marmot - Inverse symmetry. If you start at (-\infty,0) then it rises to (0,1/2) and (\infty,1). – John Kormylo Feb 20 '19 at 17:32
@JohnKormylo I am not convinced. (Yes, a function that is continuous, goes to 0 at -\infty and 1 at \infty will be 1/2 somewhere, but the slope of erf has a symmetry that the screen shot does not have. ) You could add a solution that uses erf and provides a fit to the OP's screen shot to convince me. – Feb 20 '19 at 17:43

John Kormylo · Answer 3 · 2019-02-20T21:55:21.273

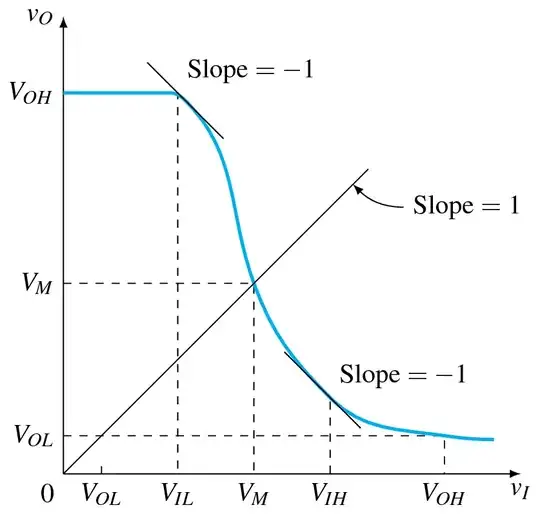
I arbitrarily chose V_M to be 2.5 and scaled the curve to go from 0.5 to 4.5.

To locate where the slope equals 1, you take the scale factor for x divided by the scale factor for y (or 0.125 in this case) and locate where the Gaussian equals 0.125 (about x=1.52) and convert back to axis units.

I copied the table by hand from a CRC handbook. (You're welcome.)

\begin{filecontents}{gauss.csv}
x,p,erf
0.00,0.3989,0.0000
0.05,0.3984,0.0199
0.10,0.3970,0.0398
0.15,0.3945,0.0596
0.20,0.3910,0.0793
0.25,0.3867,0.0987
0.30,0.3814,0.1179
0.35,0.3752,0.1368
0.40,0.3683,0.1554
0.45,0.3605,0.1736
0.50,0.3521,0.1915
0.55,0.3429,0.2088
0.60,0.3332,0.2258
0.65,0.3230,0.2422
0.70,0.3123,0.2580
0.75,0.3011,0.2734
0.80,0.2897,0.2881
0.85,0.2780,0.3023
0.90,0.2661,0.3159
0.95,0.2541,0.3289
1.00,0.2420,0.3413
1.05,0.2299,0.3531
1.10,0.2179,0.3643
1.15,0.2059,0.3749
1.20,0.1942,0.3849
1.25,0.1827,0.3944
1.30,0.1713,0.4032
1.35,0.1604,0.4115
1.40,0.1497,0.4192
1.45,0.1394,0.4265
1.50,0.1295,0.4332
1.55,0.1200,0.4394
1.60,0.1109,0.4452
1.65,0.1023,0.4505
1.70,0.0941,0.4554
1.75,0.0863,0.4599
1.80,0.0790,0.4641
1.85,0.0721,0.4678
1.90,0.0656,0.4713
1.95,0.0596,0.4740
2.00,0.0540,0.4773
2.05,0.0488,0.4798
2.10,0.0440,0.4821
2.15,0.0396,0.4842
2.20,0.0355,0.4861
2.25,0.0317,0.4878
2.30,0.0283,0.4893
2.35,0.0252,0.4906
2.40,0.0224,0.4918
2.45,0.0198,0.4929
2.50,0.0175,0.4938
2.55,0.0155,0.4946
2.60,0.0136,0.4953
2.65,0.0119,0.4950
2.70,0.0104,0.4965
2.75,0.0091,0.4970
2.80,0.0079,0.4974
2.85,0.0069,0.4978
2.90,0.0060,0.4981
2.95,0.0051,0.4984
3.00,0.0044,0.4987
\end{filecontents}
\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{intersections}
\usepackage{pgfplots,pgfplotstable}
\begin{document}
\pgfplotstableread[col sep=comma]{gauss.csv}\rawtable
\begin{tikzpicture}
\begin{axis}[axis x line=bottom, axis y line=left, clip=false,
    xtick=\empty, ytick=\empty,
    xmin=0, xmax=5, ymin=0, ymax=5]
  \addplot[thick,color=cyan,no marks] coordinates {(0,4.5) (1,4.4948)};
  \addplot[thick,color=cyan,no marks] table[x expr={2.5-0.5*\thisrow{x}},
    y expr={2.5+4*\thisrow{erf}}] {\rawtable};
  \addplot[thick,color=cyan,no marks] table[x expr={2.5+0.5*\thisrow{x}},
    y expr={2.5-4*\thisrow{erf}}] {\rawtable};
  \addplot[thick,color=cyan,no marks] coordinates {(4,0.5025) (5,0.5)};
  \node[left] at (axis cs: 0,4.5) {$V_{0H}$};
  \draw[dashed] (axis cs: 4.5,0) node[below] {$V_{0H}$} -- (axis cs: 4.5,0.5025);
  \draw[dashed] (axis cs: 0,0.5025) node[left] {$V_{0L}$}  -- (axis cs: 4.5,0.5025);
  \draw (axis cs: 0.5025,0) node[below] {$V_{0L}$}  -- (axis cs: 0.5025,0.1);
  \draw (axis cs: 0,0) -- (axis cs: 4,4);
  \draw[dashed] (axis cs: 2.5,0) node[below] {$V_M$} -- (axis cs: 2.5,2.5);
  \draw[dashed] (axis cs: 0,2.5) node[left] {$V_M$} -- (axis cs: 2.5,2.5);
  \draw[dashed] (axis cs: 1.75,0) node[below] {$V_{1L}$} -- (axis cs: 1.75,4.2428);
  \draw (axis cs: 1.5,4.4928) -- (axis cs: 2.0, 3.9928);
  \draw[dashed] (axis cs: 3.25,0) node[below] {$V_{2L}$} -- (axis cs: 3.25,0.7572);
  \draw (axis cs: 3.0,1.0072) -- (axis cs: 3.5, 0.5072);
  \end{axis}
\end{tikzpicture}
\end{document}

John your answer is a treat. To be honest, I don't know what a CRC handbook is so after googling it, I assune there is a book in which one can find the detailed graphing of a NOT gate transfer characteristic as a table and not as an explicit expression like in @marmot's answer above. Is that correct? — billyandriam, Feb 22 '19 at 00:50
Did you find https://en.wikipedia.org/wiki/CRC_Handbook_of_Chemistry_and_Physics? As stated, the table contains the Gaussian distribution and error function. This is not to say that the handbook doesn't contain BJT tables, but I didn't actually look. — John Kormylo, Feb 22 '19 at 18:06

Drawing a function without knowing its definition

3 Answers3

Important Note

Linked