Circle made from intersecting spheres

Question

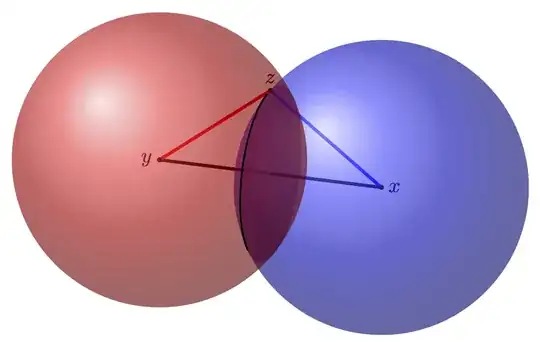
I'm trying to make a diagram along the lines of what I have below:

• 2 intersecting spheres with centers of x and y
• Midpoint is (x+y)/2 and from either center to midpoint is d/2
• Distance from centers to point of intersection is r

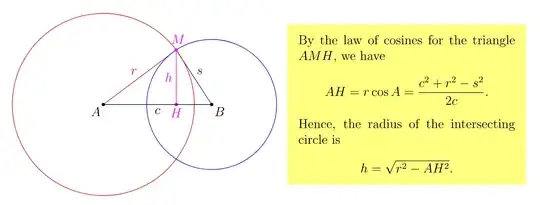
I want to show that all the intersections of the two spheres lie on a plane that is perpendicular to the line connecting the midpoints, the plane passes through the midpoint, and all the intersection points of the two spheres makes a circle.

Now I actually could somewhat make this if I just made it 2D (rather than using paint, I'd use tikz), but I'm wondering if this could be made into 3D without having it seem too busy.

So far, with the help of Schrodinger's Cat, I've got this (but I'll be working on it since this is the first 3d tikz I've tried to make):

\documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot-circleofsphere} 
\begin{document} 
\tdplotsetmaincoords{70}{200}
\begin{tikzpicture}[tdplot_main_coords,declare function={d=4;R=2.5;}]
\path (0,0,0) coordinate (x) (d,0,0) coordinate (y);
\begin{scope}[tdplot_screen_coords] 
\path[ball color=blue,opacity=0.3] (x) circle[radius=R*1cm]; 
\path[ball color=blue,opacity=1.0] (x) circle[radius=R*0.02cm]; 
\path[ball color=red,opacity=0.3] (y) circle[radius=R*1cm]; 
\path[ball color=red,opacity=1.0] (y) circle[radius=R*0.02cm]; 
\node(draw) at (0.5,0,0) {y};
\node(draw) at (-4.2,0.5,0) {x};
\node(draw) at (-1.8,2,0) {z};
\draw[black, ultra thick] (x) -- (y);
\draw[blue, ultra thick] (x) -- (-1.7,1.7);
\draw[red, ultra thick] (y) -- (-1.7,1.7);
\end{scope} 
\tdplotCsDrawCircle[tdplotCsFront/.style={thick}]{R}{0}{90}{90-atan2(sqrt(R*R-d*d/4),d/2)} 
\end{tikzpicture} 
\end{document}

Answer 1

This is my spelled out comment with some additional ingredients that resemble your own additions. This code relies on tikz-3dplot-circleofsphere, which can be found here.

\documentclass[tikz,border=3mm]{standalone} 
\usepackage{tikz-3dplot-circleofsphere} 
\begin{document} 
\tdplotsetmaincoords{70}{200}
\begin{tikzpicture}[tdplot_main_coords,declare function={d=4;R=2.5;}]
  \path (0,0,0) coordinate[label=right:$x$] (x) 
      (d,0,0) coordinate[label=left:$y$] (y)
      (d/2,0,{sqrt(R*R-d*d/4)}) coordinate[label=above:$z$] (z);
  \draw[black, ultra thick] (y) -- (d/2,0,0);
  \draw[red, ultra thick] (y) -- (z);   
  \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,fill=gray,fill opacity=0.7},
      tdplotCsBack/.style={thin,gray,fill=gray,fill opacity=0.7}]{R}{0}{90}{90-atan2(sqrt(R*R-d*d/4),d/2)} 
  \draw[black, ultra thick] (x) -- (d/2,0,0);
  \draw[blue, ultra thick] (x) -- (z);
  \fill foreach \X in {x,y,z} {(\X) circle[radius=1.2pt]};
  \begin{scope}[tdplot_screen_coords] 
    \path[ball color=blue,opacity=0.6] (x) circle[radius=R*1cm]; 
    \path[ball color=red,opacity=0.6] (y) circle[radius=R*1cm]; 
  \end{scope} 
  \tdplotCsDrawCircle[tdplotCsFront/.style={thick},
      tdplotCsBack/.style={draw=none}]{R}{0}{90}{90-atan2(sqrt(R*R-d*d/4),d/2)} 
\end{tikzpicture} 
\end{document}

Answer 2

This is not an answer. I want to show the way to draw the circle is intersection of two spheres based on the answer here.

I choose two spheres have equations (x - 3)^2 + (y + 4)^2 + z^2 = 64 and (x - 3)^2 + (y - 2)^2 + (z - 8)^2 = 36. My code

\documentclass[tikz,border=2mm, 12 pt]{standalone}
\usepackage{tikz-3dplot-circleofsphere}
\usetikzlibrary{3dtools} 
\begin{document}
\tdplotsetmaincoords{70}{100}
\begin{tikzpicture}[scale=1,tdplot_main_coords,declare function={R=8;R1=6;
}]
\path (3,-4,8) coordinate (A)
({(9-sqrt(95))/3},8/3,3) coordinate (B)
({(9+sqrt(95))/3},8/3,3) coordinate (C)
(3,2,8) coordinate (T)
(3,-4,0) coordinate (I);
\begin{scope}[tdplot_screen_coords]
 \fill[ball color=red,opacity=0.6] (I) circle (R);
 \fill[ball color=green!50, opacity=1.0] (T) circle (R1);
\end{scope}
\foreach \p in {A,B,C,I,T}
\draw[fill=black] (\p) circle (1.5pt);
\foreach \p/\g in {A/90,C/-90,B/-90,I/-90,T/90}
\path (\p)+(\g:3mm) node{$\p$};
\pic[draw=none]{3d circle through 3 points={A={(A)},B={(B)},C={(C)}}};
\begin{scope}[shift={(T)}]
\path[overlay] [3d coordinate={(myn)=(A)-(B)x(A)-(C)},
3d coordinate={(A-M)=(A)-(M)}];
\pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")}
\pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]}
\pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]}
\pgfmathsetmacro{\mygamma}{acos(sqrt(TD("(A-M)o(A-M)"))/R1)}
\tdplotCsDrawCircle[tdplotCsFront/.style={thick,red}]{R1}{\myalpha}{\mybeta}{\mygamma}  
\end{scope}
\end{tikzpicture}
\end{document}

Answer 3

Here is solution for general case when 2 possibly different radii. First we calculate as in the planar figure

// http://asymptote.ualberta.ca/
usepackage("ragged2e"); // for justify command
usepackage("amsmath");
unitsize(7mm);
real r=4.2, s=3; // two radii
real c=5;     // distance of two centers
pair A=(0,0), B=c*dir(0);   //two centers 
pair M=intersectionpoints(circle(A,r),circle(B,s))[0];
real dAH=(c^2+r^2-s^2)/(2*c);
real h=sqrt(r^2-dAH^2);
pair H=A+dAH*unit(B-A);
draw(Label("$h$",align=W),M--H,magenta);
draw(Label("$r$",align=NW),A--M,red);
draw(Label("$s$",align=NE),B--M,blue);
draw(circle(A,r),red);
draw(circle(B,s),blue);
dot(H^^M,magenta);
dot("$A$",A,SW);
dot("$B$",B,SE);
label("$M$",M+.5dir(80),magenta);
label("$H$",H,S,magenta);
draw(Label("$c$"),A--B);
string explanation=minipage("\justify{
By the law of cosines for the triangle $AMH$, we have
$$AH=r \cos A=\dfrac{c^2+r^2-s^2}{2c}.$$
Hence, the radius of the intersecting circle is
$$h=\sqrt{r^2-AH^2}.$$
}",7cm);
label(explanation,point(E)+(6,0),Fill(3mm,lightyellow));
shipout(bbox(5mm,invisible));

And now things are translated to 3D, different from https://tex.stackexchange.com/a/121900/140722. Module graph3 is for better accuracy of the intersecting circle Circle(H,h,normal=B-A).

// http://asymptote.ualberta.ca/ 
unitsize(1cm);
//import math;
//import three;
import graph3; // implicitly import math and three;
real r=3.5, s=4; // two radii
real c=5;     // distance of two centers
triple A=(0,0,0), B=cdir(90,90);   //two centers 
surface sphAr=shift(A)scale3(r)unitsphere;
surface sphBs=shift(B)scale3(s)*unitsphere;
draw(sphAr,red+opacity(.2));
draw(sphBs,blue+opacity(.2));
real dAH=(c^2+r^2-s^2)/(2c);
real h=sqrt(r^2-dAH^2);
triple H=A+dAHunit(B-A);
draw(Circle(H,h,normal=B-A),magenta+1pt);
dot(H,magenta);
dot("$A$",A,W);
dot("$B$",B);
draw(A--B);
//axes3("$x$","$y$","$z$");