Update: The calculations are from the 3-D Cartesian true range multilateration (in fact, those are formulae for calculating intersections of three spheres). I also add the 3D grid on XY-plane.

unitsize(1cm);
import three;
import grid3;
triple barycentric(triple A, triple B, triple C, real a, real b, real c){return (a*A+b*B+c*C)/(a+b+c);}
currentprojection=orthographic((1,1,.8),center=true,zoom=.9);
// Step 1: construct the base A,B,C on the plane z=0
real a=5, b=4, c=3;
triple B=(0,0,0), C=(a,0,0);
// Abc is the projection of A on the segment BC
triple Abc=barycentric(B,C,O,1/(a^2+c^2-b^2),1/(a^2+b^2-c^2),0);
real bt=abs(Abc-B);
real hbc=sqrt(cc-btbt);
triple A=Abc+hbc*dir(90,90);
draw(A--B--C--cycle,blue+1pt);
label("$A$",A,plain.S);
label("$B$",B,dir(150));
label("$C$",C,plain.NW);
//label("$A_{bc}$",Abc,plain.N,red);
//draw(A--Abc,red);
// Step 2: get the top point D
real at=6, bt=7, ct=8;
// H is the projection of D on the base ABC
// https://en.wikipedia.org/wiki/True-range_multilateration
real Hx=(bt^2-ct^2+a^2)/(2a);
real Hy=(bt^2-at^2+A.x^2+A.y^2-2A.x*Hx)/(2A.y);
real Dz=sqrt(bt^2-Hx^2-Hy^2);
triple H=(Hx,Hy,0);
triple D=(Hx,Hy,Dz);
draw(D--A^^D--B^^D--C,blue+1pt);
draw(D--H,red+dashed);
label("$D$",D,plain.N);
label("$H$",H,plain.E,red); dot(H,red);
// grid on XY-plane
limits((-2,-2,0),(7,5,0));
grid3(XYXgrid,step=1,.5gray+.5white);
draw(Label("$x$",EndPoint),O--8X,Arrow3());
draw(Label("$y$",EndPoint),O--6Y,Arrow3());
draw(Label("$z$",EndPoint),O--6Z,Arrow3());
write("H = ("+string(H.x)+","+string(H.y)+",0)");
write("DH = "+string(abs(H-D)));

Old answer This is a well-known construction problem of Euclidean geometry. In drawing, we can use geometric constructions, but it is better to use computation approaches. Among some computation approaches, I found one using barycentric coordinate is more convenient and can be applied for drawing both 2D and 3D figures.
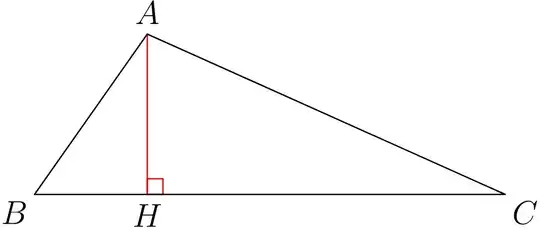
Problem 1. Triangle on the plane: To construct a triangle ABC on the plane Oxy knowing its 3 lengths a=BC, b=CA, c=AB (provided that the triangle a + b > c is fulfilled)
The usual way is first taking B and C such that BC=a, then A is one of two intersection points of the circle centered B with radius c and the circle centered C with radius b, using some built-in procedures to find intersection of 2 circle path. Here I go with computation approach
using barycentric coordinate
pair barycentric(pair A=(0,0), pair B=(0,0), real a=1, real b=0){
return (a*A+b*B)/(a+b);}
Rewriting the formula in this my answer, to get the projection H of the A on BC
pair H=barycentric(B,C,1/(a^2+c^2-b^2),1/(a^2+b^2-c^2));
Finally, the point A is obtained by the Pythagorean theorem in the right triangle AHB.
// http://asymptote.ualberta.ca/
pair barycentric(pair A=(0,0), pair B=(0,0), real a=1, real b=0){
return (a*A+b*B)/(a+b);}
// Application: construct a triangle knowing the lengths of 3 sides
unitsize(1cm);
real a=6, b=5, c=2.5;
pair B=(0,0), C=(a,0);
pair H=barycentric(B,C,1/(a^2+c^2-b^2),1/(a^2+b^2-c^2));
real bt=abs(H-B);
real h=sqrt(cc-btbt);
pair A=H+h*dir(90);
draw(box(H,H+(.2,.2)),red);
draw(A--H,red);
draw(A--B--C--cycle);
label("$A$",A,plain.N);
label("$B$",B,plain.SW);
label("$C$",C,plain.SE);
label("$H$",H,plain.S);
Problem 2. Triangle on the space: To construct a triangle ABC on the space Oxyz knowing its 3 lengths a=BC, b=CA, c=AB (provided that the triangle inequality a + b > c is fulfilled)
This can be done as same as Problem 1 with suitable minor changes (see Step 1 in the code of Problem 3 below).
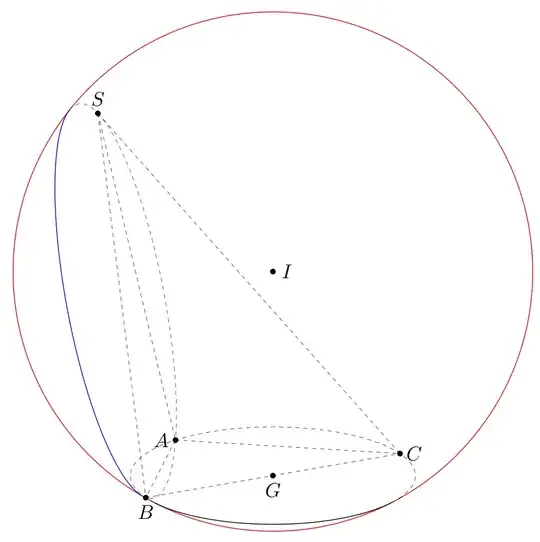
Problem 3. Tetrahedron on the space: To construct a tetrahedron D.ABC on the space Oxyz knowing its 6 lengths (3 lengths of the base a=BC, b=CA, c=AB; and 3 remaining lengths at=DA, bt=DB, ct=DC (provided that some conditions are fulfilled, see this 2009 EMS paper).
We use barycentric coordinate 2 times. First construct triangle ABC on some plane, say z=0. This is the above Problem 2. Next, get the projection H of D on the base ABC. The Heron formula is used in the barycentric coordinates of H (areas are used instead of side lengths)
import three;
triple barycentric(triple A, triple B, triple C, real a, real b, real c){return (a*A+b*B+c*C)/(a+b+c);}
real Heron(real a, real b, real c){
real p=(a+b+c)/2;
return sqrt(p(p-a)(p-b)*(p-c));
}
then the desired point D is obtained by the Pythagoras theorem in the right triangle DHA.

Full code (still some mistake! I am looking for barycentric coordinates of the foot of an altitude in a tetrahedron - seems an interesting and sensitive situation)
unitsize(1cm);
import three;
triple barycentric(triple A, triple B, triple C, real a, real b, real c){return (a*A+b*B+c*C)/(a+b+c);}
real Heron(real a, real b, real c){
real p=(a+b+c)/2;
return sqrt(p(p-a)(p-b)*(p-c));
}
currentprojection=orthographic((1,1.6,1),center=true,zoom=.95);
// Step 1: construct the base A,B,C on the plane z=0
real a=6, b=5, c=4;
triple B=(0,0,0), C=(a,0,0);
// Abc is the projection of A on the segment BC
triple Abc=barycentric(B,C,O,1/(a^2+c^2-b^2),1/(a^2+b^2-c^2),0);
real bt=abs(Abc-B);
real hbc=sqrt(cc-btbt);
triple A=Abc+hbc*dir(90,90);
draw(A--Abc,red);
draw(A--B--C--cycle);
label("$A$",A,plain.S);
label("$B$",B,plain.E);
label("$C$",C,plain.W);
label("$A_{bc}$",Abc,plain.N,red);
// Step 2: get the top point D
real at=6, bt=7, ct=4;
// H is the projection of D on the base ABC
real Sdab=Heron(at,bt,c);
real Sdbc=Heron(bt,ct,a);
real Sdca=Heron(ct,at,b);
triple H=barycentric(A,B,C,1/(Sdab^2+Sdca^2-Sdbc^2),1/(Sdab^2+Sdbc^2-Sdca^2),1/(Sdca^2+Sdbc^2-Sdab^2));
real ha=abs(H-A);
real hd=sqrt(atat-haha);
triple D=H+hd*Z;
draw(D--A^^D--B^^D--C);
draw(D--H,blue);
label("$D$",D,plain.N);
label("$H$",H,plain.W,blue); dot(H);
PS1: Why Asymptote and why not TikZ? That drawing way of using barycentric coordinate can be coded in several drawing languages. TikZ does has barycentric coordinate; but its computation is quite weak, Dimension too large error may happen, even in 2D when I had tried drawing the Euler line of a triangle)! Asymptote has better accuracy, and available for 3D.
PS2: There is another way based on origami, described in a book of Polya. I will do it in free time later.







3,4,5,6,7,8are sides of a tetrahedron? Note that fora,b,cbe 3 sides of a triangle, we need the triangle inequalitya+b>c. There is a similar situation for tetrahedron, see this paper Edge lengths determining tetrahedrons https://www.ems-ph.org/journals/show_abstract.php?issn=0013-6018&vol=64&iss=4&rank=4 – Black Mild Oct 03 '21 at 09:51