1

I am preparing a note for Weierstrass's approximation theorem. There I am stuck with the graphs of the iterated functions generated in the process. How do I draw them in tikz? Following are my data:

enter image description here

I need the graphs for n = 5, 15, 25 and 35. I have made the graphs in Desmos for your compliance. Please find it here. Following is an MWE:

\documentclass{article}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{tikz}

\begin{document}
    \begin{align*}
        f(x)    &=  (\sin x)(\sin \pi x), &&    0\le x\le 1\\[1ex]
        Q_n(x)  &=  \frac{(1-x^{2})^{n}}{\int_{-1}^{1}(1-t^{2})^{n}\,dt}, &&    -1\le x\le 1\\[1ex]
        P_n(x)  &=  \int_{0}^{1}f(t)Q_{n}(t-x)dt, &&    0\le x\le 1.
    \end{align*}
    \begin{tikzpicture}[xscale=10, yscale=2]
        \draw (-0.05,0) -- (1.1,0) node[right] {$x$};
        \draw (0,-1.2) -- (0,1.2);
        \draw [ultra thin, domain=0:1,samples=5000] plot (\x, {sin(\x r)*sin(pi*\x r)});
        \draw (0,1) node[left] {\scriptsize$ (0,1) $} (0,-1) node[left] {\scriptsize$ (0,-1) $};
    \end{tikzpicture}
\end{document}
Subhajit Paul
  • 760
  • 1
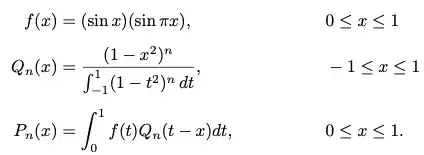
    Please do not post screen shots of functions, the very least you could do is to post copyable versions of the functions. The screen shots do not even agree with the link, Q_n has a numerator \int_{-1}^1(1-t^2)^n\,\mathrm{d}t (note the ^n). And you cannot do numerical integration easily with LaTeX, so I am not sure if this is a good idea anyway. –  May 28 '20 at 16:39
  • @Schrödinger'scat, I am extremely sorry for the mistake. I am editing my question with an MWE. – Subhajit Paul May 28 '20 at 16:44
  • 1
    This leaves us with the problem that one cannot do numerical integrations so it will be extremely hard to do that with LaTeX only. –  May 28 '20 at 17:12
  • @Schrödinger'scat, can we approximate using Riemann sum? Suppose we divide the interval [0,1] into 500 subintervals. For each x from 0 to 500 plot the area of f(t)Q_{n}(t-x) using Riemann sum subdividing [0,1] into say 10 subintervals? Total number of calculation will be 5000 in that case. – Subhajit Paul May 28 '20 at 17:29
  • 2
    Yes, something like that. As I said, extremely hard, and not very accurate. So it is doable in principle, with a large amount of computation time and coding efforts, and shaky results. I'd rather create the data with Mathematica, say, and plot it with pgfplots if you need a LaTeX plot here. –  May 28 '20 at 17:35
  • @Schrödinger'scat I do not mind at all. That will also be extremely helpful. I only need the output in my book and not the codes. – Subhajit Paul May 28 '20 at 17:40

0 Answers0