3

Graphs of iterated functions in Weierstrass's approximation theorem

I have a problem while drawing the following functions:

enter image description here

Here is my code:

import graph;
size(8cm,6cm,false);

real F(real x){return sin(x)sin(pix);}


typedef real integral(real);


integral G(int n){return new real(real x){
                            return ((1-x^2)^n)/(simpson(new real(real t){return (1-t^2)^n;},-1,1));}; }


integral Pnx(int n){return new real(real x){ // I think it is right!
                            return simpson(new real(real t){return F(t)*G(n)(t-x);},0,1);}; }


draw(Label("$x$",EndPoint),(-2,0)--(2,0),Arrow);
draw(Label("$y$",EndPoint),(0,-2)--(0,4),Arrow);
int smooth=400;
path f=graph(F,0,1,smooth);
draw(f,brown);


pen pe[]={red,green,blue,cyan,magenta,pink,gray};
pe.cyclic=true;
path g;
for (int i : new int[]{5,10,15,20,25,30,35}){
g=graph(G(i),-1,1,smooth);
draw(g,pe[i]);
}


// path h=graph(Pnx(5),0,1,smooth); // can't draw
// draw(h,blue); // can't draw

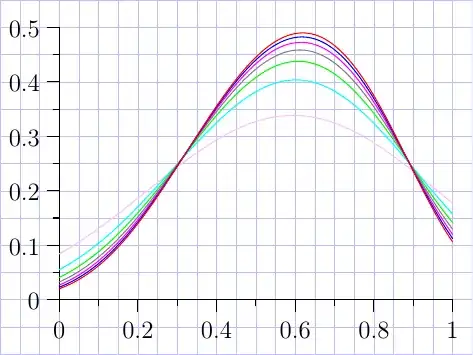
The output:

cbcb

Question:

Is my computer weak to draw this function?

  • 3
    Pure asymptote questions are off topic here, please ask this question on a web page handling asymptote ... – Mensch Jul 22 '20 at 09:32
  • 8
    @Mensch: Please, not again. Your opinion is wrong and insulting, Pure asymptote questions are on topic here.

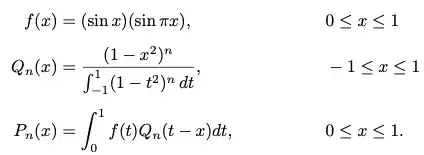
    Questions tagged [asymptote]

    Asymptote is a TeX-aware vector graphics language with built-in 3D capabilities. This tag, which is compatible with the [diagrams] tag, may be used for questions about drawing diagrams. It is also appropriate for questions about the asymptote package, which allows Asymptote code to be included directly in .tex files.

    And anybody are free to answer to such questions using alternative drawing tools, like for example, metapost or pstricks.

     – g.kov Jul 22 '20 at 18:05

1 Answers1

5

Try this one:

settings.tex="pdflatex";
import math;
import graph;
size(8cm,6cm,false);
real sc=0.05;
add(shift(-3*sc,-2*sc)*scale(sc)*grid(24,13,paleblue+0.2bp));
real xmin=0,xmax=1;
real ymin=0,ymax=0.5;
xaxis(xmin,xmax,RightTicks(Step=0.2,step=0.1),above=true);
yaxis(ymin,ymax,LeftTicks (Step=0.1,step=0.05),above=true);

real F(real x){return sin(x)sin(pix);}
typedef real realFreal(real);
real sqrtPi=sqrt(pi);
realFreal Q(int n){ // int((1-t^2)^n,t=-1..1)
                    //   = sqrt(pi)gamma(n+1)/gamma(n+3/2) 
  return 
    new real(real x){
      return (1-x^2)^ngamma(n+3/2)/gamma(n+1)/sqrtPi;
    }; 
}
realFreal FPn(int n, real x){
  real c=gamma(n+3/2)/gamma(n+1)/sqrt(pi);
  return new real(real t){return csin(t)sin(pit)(1-(t-x)^2)^n;};
}
realFreal Pn(int n){
  return new real(real x){return simpson(FPn(n,x),0,1);};
}


int smooth=400;
pen pe[]={red,green,blue,cyan,magenta,pink,gray}; pe.cyclic=true;


path g;
for (int ni : new int[]{5,10,15,20,25,30,35}){
  g=graph(Pn(ni),0,1,smooth);
  draw(g,pe[ni]);
}

enter image description here

g.kov
  • 21,864
  • 1
  • 58
  • 95
  • Why do we need change expression ? –  Jul 22 '20 at 20:02
  • @user213378: Integral in the denominator of Qn(x) has an explicit solution, we don't need to use simpson to solve it numerically. – g.kov Jul 22 '20 at 20:18
  • I wish I had these représentations of these polynoms when I was a student! – JeT Jul 22 '20 at 20:28
  • @g.kov You can read it. Thanks for texpath from here. –  Aug 01 '20 at 10:39
  • @g.kov You can tell me know the mathematical knowledge of this transformation? What is it? int((1-t^2)^n,t=-1..1)= sqrt(pi)*gamma(n+1)/gamma(n+3/2). This is the first time I have seen it. :-( –  Aug 20 '20 at 11:11
  • 1
    @user213378: It's just a known definite integral, see WolframAlpha. – g.kov Aug 20 '20 at 11:56