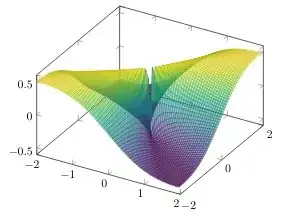
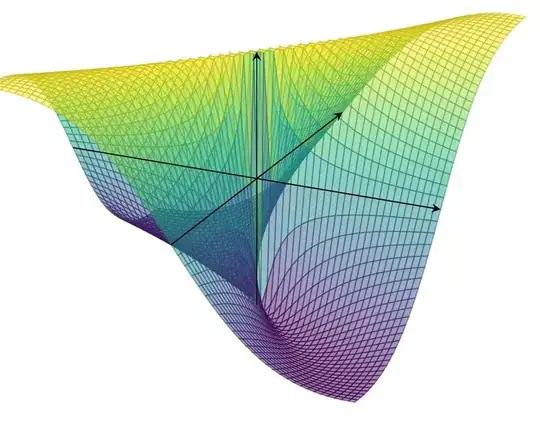
I would like to plot the function f: ℝ² →ℝ, definited by f(x,y)=(xy)/(x^2+y^2). But the following problem comes up:
At (0,0) the function is not continous and therefore it looks kind of jagged.
To solve this problem i could force the function to input specific points but i can't find it anywhere an don't know if that is even possible.
Code:
\begin{tikzpicture}[]
\begin{axis}[axis lines=center,
axis on top,
xtick=\empty,
ytick=\empty,
ztick=\empty,
xrange=-2:2,
yrange=-2:2
]
% function
\addplot3[domain=-2:2,y domain=-2:2,colormap/viridis,surf,opacity=0.5,samples = 55]
{(x*y)/(x^2+y^2)};
\end{axis}
\end{tikzpicture}
How do i make this function look smooth? Any help would be greatly appreciated :)
(Just increasing the Samples doesnt do that much, and I run into the following error: TeX capacity exceeded, sorry [main memory size=3000000])




x=y=0is undefined. The problem is avoided by letting TikZ decide whatatan2(0,0)is. You can choose another prescription, which is what the OP did in their own answer. Neither prescription is "correct". The issue addressed here is to get rid of the fake pole, which the answer does. – Jun 01 '20 at 14:50atan2confuse me sometimes... but they are very useful to avoid singularities – BambOo Jun 01 '20 at 15:20something/0), it is just that pgfplots thinks there is one simply because the denominator becomes 0 forx=y=0. In the polar representation one can see that the expression is finite forx=y=0. It is, however, not well-defined or uniquely defined as it is basically determined by the phase of the complex numberz=0. – Jun 01 '20 at 15:47A*cos(x)+B*sin(x)transformed into a singleC*sin(x+\phi):) – BambOo Jun 01 '20 at 15:52