Draw 3D Cube knowing 3 points

Question

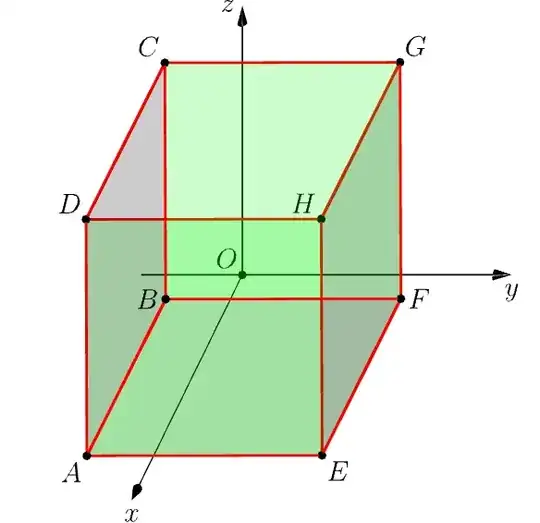
I need to draw this figure and I only know the coordinates of points A(11,-1,2), B(13,2,8) and E(8,5,0).

Answer 1

You can use cross products to compute the other corners.

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[tdplot_main_coords,line join = round, line cap = round,
    declare function={Ax=11;Ay=-1;Az=2;Bx=13;By=2;Bz=8;Ex=8;Ey=5;Ez=0;
        Fx=Ex+Bx-Ax;Fy=Ey+By-Ay;Fz=Ez+Bz-Az;}]
 \begin{scope}
   \pgfmathsetmacro{\myn}{sqrt(pow(Bx-Ax,2)+pow(By-Ay,2)+pow(Bz-Az,2))}
   \def\tdplotcrossprod(#1,#2,#3)(#4,#5,#6){%
        \pgfmathsetmacro{\tdplotresx}{(#2) * (#6) - (#3) * (#5)}% 
        \pgfmathsetmacro{\tdplotresy}{(#3) * (#4) - (#1) * (#6)}% 
        \pgfmathsetmacro {\tdplotresz }{(#1) * (#5) - (#2) * (#4)}}
   \tdplotcrossprod(Bx-Ax,By-Ay,Bz-Az)(Ex-Ax,Ey-Ay,Ez-Az)       
   \pgfmathsetmacro{\mynx}{\tdplotresx/\myn}
   \pgfmathsetmacro{\myny}{\tdplotresy/\myn}
   \pgfmathsetmacro{\mynz}{\tdplotresz/\myn}
   \path (Ax,Ay,Az) coordinate[label=left:{$A$}] (A) 
     (Bx,By,Bz) coordinate[label=above left:{$B$}] (B)
     (Ex,Ey,Ez) coordinate[label=right:{$E$}] (E) 
     (Fx,Fy,Fz) coordinate[label=right:{$F$}] (F)
     (Ax+\mynx,Ay+\myny,Az+\mynz) coordinate[label=left:{$D$}] (D) 
     (Bx+\mynx,By+\myny,Bz+\mynz) coordinate[label=left:{$C$}] (C)
     (Fx+\mynx,Fy+\myny,Fz+\mynz) coordinate[label=right:{$G$}] (G)
     (0,0,0) coordinate (O)
     (15,0,0) coordinate[label=left:{$x$}] (ex)
     (0,10,0) coordinate[label=right:{$y$}] (ey)
     (0,0,10) coordinate[label=right:{$z$}] (ez);
 \end{scope}    
 \draw[thick] (A) -- (B) -- (F) -- (E) -- cycle
  (A) -- (D) -- (C) -- (B) (C) -- (G) -- (F); 
 \begin{scope}
  \clip (A) --(D) -- (C) -- (G) -- (F) -- (E) -- cycle 
  (current bounding box.south west) -| (current bounding box.north east) -| cycle;
  \draw[very thick,-stealth] (O) -- (ex);
  \draw[very thick,thick,-stealth] (O) -- (ey);
  \draw[very thick,thick,-stealth] (O) -- (ez);
 \end{scope}
 \begin{scope}
  \clip (A) --(D) -- (C) -- (G) -- (F) -- (E) -- cycle ;
  \draw[dashed] (O) -- (ex);
  \draw[dashed] (O) -- (ey);
  \draw[dashed] (O) -- (ez);
 \end{scope}
\end{tikzpicture}
\end{document}

Answer 2

Merry Xmas!

Hidden lines hide, so in fact we can not see the hidden lines unless there is some transperancy. Dashed line are just a convention for expressing hidden lines. A dashed line is not real, and a hidden line is real, but hidden. Dashed lines are mostly used with black-white figures in the past. Dashed is not the only convention: think about hidden surface and dashed surface (what are they ? ^^). We may use colors, opacity/transparency, lightning as another ways of expressing hidden lines and hidden surfaces.

In Asymptote with module three, I just draw/fill things as they are, that is, easy, relaxing for brain, no tricky. More precisely, I use opacity(.5) for filling faces of the cube. 3D effects are just great. You can see the labels O and H are transparent because they are hidden; the label B is normal, because B is visible. A usual built-in calculations are as follows.

• cross(B-A,E-A) is the vector of the cross product of vector AB and AE;
• unit(u) gives the unit vector in the direction of vector u;
• a=length(B-A) is the length of vector AB, i.e., the length of the side of the cube; therefore
• D=A+a*unit(cross(B-A,E-A)) is the vertex D of the cube ABCD EFGH;

// http://asymptote.ualberta.ca/
unitsize(5mm);
//import three;
import graph3;
currentprojection=obliqueX(55);
currentprojection.center=true;
//currentlight=nolight;  //  not working ? 
// vertexes of the cube
triple A=(11,-1,2), B=(13,2,8), E=(8,5,0), F=B+E-A;
real a=length(A-B);
triple D=A+a*unit(cross(B-A,E-A)), C=D+B-A;
triple G=C+F-B, H=G+E-F;
// pens for filling and drawing surfaces
pen pfill=green+opacity(.2);   // change opacity as you wish
pen pdraw=red+linewidth(1pt);
// define a command to fill and draw a face
void Drawface(triple A,triple B,triple C, triple D){
draw(surface(A--B--C--D--cycle),pfill);
draw(A--B--C--D--cycle,pdraw); 
}
// now come those faces
Drawface(B,C,G,F);Drawface(A,B,F,E);
Drawface(A,B,C,D);Drawface(E,F,G,H);
Drawface(A,D,H,E);
// labeling
dot("$A$",A,plain.SW);dot("$B$",B,plain.W);
dot("$C$",C,plain.NW);dot("$D$",D,plain.NW);
dot("$E$",E,plain.SE);dot("$F$",F,plain.E);
dot("$G$",G,plain.NE);dot("$H$",H,plain.NW);
dot("$O$",O,plain.NW);
// axes
//draw(Label("$x$",EndPoint),O--12X,Arrow3);
//draw(Label("$y$",EndPoint),O--10Y,Arrow3);
//draw(Label("$z$",EndPoint),O--8Z,Arrow3);
axes3("$x$","$y$","$z$",max=(10,8,8),Arrow3);