When writing an integral, it seems like something should be done to separate the "d", as in \int f(x) dx, so as not to confuse it with a variable. I've seen it left as-is, bolded, and straightened. Even among those options there are several ways to accomplish each task; e.g., I could do a \mathrm or a \operatorname. What is the preferred method of dealing with the "d"?
7 Answers
\documentclass{article}
\usepackage{amsmath}
\newcommand*\diff{\mathop{}\!\mathrm{d}}
\newcommand*\Diff[1]{\mathop{}\!\mathrm{d^#1}}
\begin{document}
\begin{align*}
\biggl(\int_{-\infty}^\infty e^{-x^2}\diff x\biggr)^2
&= \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)}\diff x\diff y \\
&= \int_0^{2\pi}\int_0^\infty e^{-r^2}r\diff r\diff\theta \\
&= \int_0^{2\pi}\biggl(-{e^{-r^2}\over2}\bigg\vert_{r=0}^{r=\infty}\,\biggr)\diff\theta\\
&= \pi \tag*{q.e.d.}\\
\end{align*}
%
\[ V(\mathbf{x}) = -\int_{\mathbf{R}^3}
\frac{G}{|\mathbf{x}-\mathbf{y}|}\,\rho(\mathbf{y})\,\Diff3\mathbf{y} \]
\end{document}

- 11,466
-
2Herbert, are you recommending what's on the rhs? It looks odd to me, especially when I have an inline $dy/dx$. – Jim Hefferon Jun 20 '12 at 13:07
-
111IMO it makes sense to add a small explanation of why this solution was chosen, rather than just providing uncommented source code. – Marco Jun 20 '12 at 13:09
-
10if i'm not mistaken, the upright "d" is an iso standard. but it's not common practice in the u.s. (and perhaps elsewhere). certainly knuth uses -- intentionally -- an italic "d" as can be inferred from the italic correction "d" is given in the cmmi fonts, namely none. what i find peculiar in @Herbert's example is the italic "d" on the left side while upright is used on the right. in my opinion, whichever is chosen should be used consistently. – barbara beeton Jun 20 '12 at 13:19
-
@Barbara. It is, in ISO 80000-2. Note however this standard bears the title "Mathematical signs and symbols to be used in the natural sciences and technology". – Javier Bezos Jun 20 '12 at 17:29
-
2
-
@barbarabeeton: sure, they should always be upright. I forgot that one on the left. it is correct now. – Jan 28 '13 at 11:45
-
@Herbert why not just
\DeclareMathOperator\diff{d}? To be used when you have derivatives\frac{\diff x}{\diff y}or integrals\int x y \diff x \diff y? – cacamailg Jun 29 '13 at 15:58 -
@Herbert could you extend your answer to multidimensional integrals, where one could write something like
d^n xfor ann-dimensional integral. I'm asking this, because\diff^n xcreates a too large space before thexin my opinion. (Example here, last equation). – Jost Nov 05 '13 at 10:55 -
-
1Thank you, but (1) I think it should be
\newcommand*\Diff[1]{\mathop{}\!\mathrm{d}^#1}, because thenin my example should not be in roman. (2) I still find the distance between thed^nand thextoo large. Thexlooks like a regular variable. I think I would rather write\newcommand*\Diff[2]{\mathop{}\!\mathrm{d}^{#1}\!{#2}}, although it is a tad too close. – Jost Nov 05 '13 at 13:16 -
Hey, very late question but what does the
*do after\newcommand? I use mathjax usually, perhaps it is a difference? (Not lazy but http://tex.stackexchange.com/questions/1050/whats-the-difference-between-newcommand-and-newcommand doesn't seem to explain why MathJax seems to output things when * is used!) – Alec Teal Nov 24 '15 at 12:04 -
@AlecTeal: With a star the new command cannot handle paragraphs ( the command
\par) which is not really of interest here, because it has already no argument. In short: It makes no difference here with or without a star. In TeX notation: withoiut a star it is a so-called lon definition of a macro. – Dec 07 '15 at 15:47
I found a TUGboat article some years ago which seems to deal with the spacing around the differential operator in the correct way (at least to me).
Example
\documentclass{article}
\makeatletter
\providecommand*{\dif}%
{\@ifnextchar^{\DIfF}{\DIfF^{}}}
\def\DIfF^#1{%
\mathop{\mathrm{\mathstrut d}}%
\nolimits^{#1}\gobblespace
}
\def\gobblespace{%
\futurelet\diffarg\opspace}
\def\opspace{%
\let\DiffSpace\!%
\ifx\diffarg(%
\let\DiffSpace\relax
\else
\ifx\diffarg\[%
\let\DiffSpace\relax
\else
\ifx\diffarg\{%
\let\DiffSpace\relax
\fi\fi\fi\DiffSpace}
\makeatother
\begin{document}
\[
\int x \dif x
\]
\end{document}
Update
As pointed out by Enrico Gregorio and implemented by Herbert Voß, the following will do:
\documentclass{article}
\newcommand*\dif{\mathop{}\!\mathrm{d}}
\begin{document}
\[
\int x \dif x
\]
\end{document}
- 31,033
-
12Claudio Beccari later discovered that
\newcommand\dif{\mathop{}\!\mathrm{d}}does the same with much less effort. – egreg Jan 28 '13 at 16:37 -
According to http://tug.org/pipermail/texhax/2009-August/013018.html, the following by Morten Høgholm is an improved version of the large code chunk I posted:
\newcommand*\dif{ \mathop{}\nobreak \mskip-\thinmuskip\nobreak \mathrm{d} }what is best of Morten's code and the code posted by @egreg ? – Svend Tveskæg Jan 28 '13 at 17:03 -
4It's just the same, with two redundant
\nobreakthat do exactly nothing, because a line break is not possible in a math formula after a mathop atom or after\mskipglue. – egreg Jan 28 '13 at 17:07 -
Besides the fact that there is apparently a much shorter equivalent for the code: I believe
\ifx\diffarg\[%should be\ifx\diffarg[%, – cgnieder Jan 28 '13 at 23:28 -
@egreg What is the point of
\mathop{}, i.e., the first part of the improved\difcommand? – Svend Tveskæg Sep 08 '14 at 01:22 -
6@SvendTveskæg
\mathop{}provides the thin space at the left when preceded by an ordinary symbol or a closing delimiter; the “d” after it inserts another thin space that's removed with\!. – egreg Sep 08 '14 at 09:19 -
Have a look at
http://ctan.sharelatex.com/tex-archive/macros/latex/contrib/physics/physics.pdf
2.5 Derivatives
I use it and i am very happy with this package.
EDIT:
\documentclass{article}
\usepackage{amsmath}
\usepackage{physics}
\usepackage{amssymb}
\begin{document}
\begin{align}
\left(\int\limits_{-\infty}^\infty e^{-x^2} \dd{x} \right)^2
&=\int\limits_{-\infty}^\infty \int\limits_{-\infty}^\infty {e^{-(x^2+y^2)}}\dd{x}\dd{y} \\
&=\int\limits_{0}^{2\pi} \int\limits_{0}^\infty e^{-r^2}r \dd{r}\dd{\theta} \\
&=\int\limits_{0}^{2\pi} {\left(\left.-\frac{e^{-r^2}}2\right|_{r=0}^{r=\infty}\right)}\dd{\theta} \\
&=\pi
\end{align}
\begin{equation}
V(x)=-\int\limits_{\mathbb R^3} \frac G{|x-y|}\rho(y) \dd[3]{y}
\end{equation}
\end{document}

- 88,848
- 936
-
1Note that we can italicise the d's using
\usepackage[italicdiff]{physics}– Mateen Ulhaq Apr 09 '17 at 05:22
I usually do this (which I've shamefully stolen from Niel de Beaudrap and modified):
\makeatletter \renewcommand\d[1]{\ensuremath{%
\;\mathrm{d}#1\@ifnextchar\d{\!}{}}}
\makeatother
It renders nicely, especially with multiple integrals:

-
4I find this wrong under many respects. The
\;space is too much. The definition proposed by Herbert is certainly better. – egreg Jun 20 '12 at 13:08 -
@egreg: I'm curious if there are other reasons aside from
\;(perhaps you can replace it with\:, or with\mathop{}\!as in Herbet's solution) why you find the definition "wrong". As someone who is regularly doing all sorts of ad-hoc fooling around with spacing to try and better suggest logical groupings of symbols in my math typesetting, I'm interested in other people's notions of best practises. – Niel de Beaudrap Jun 20 '12 at 13:35 -
1I like this definition of
\d(taking care of subsequent differentials). Just IMO: (1)\ensuremathis completely wrong here, (2) the space is indeed to large and\mathop{}\!gives some nice-looking result. – yo' Jun 20 '12 at 13:42 -
@NieldeBeaudrap The
\ensuremathis completely useless (your code didn't have it); the\;spacing is too much (\,is correct) and testing whether another\dfollows should be omitted once a thin space instead of the thick space is used. – egreg Jun 20 '12 at 13:43 -
1@tohecz If
\mathop{}\!dis used, then the spacing for subsequent differentials will be automatically added. – egreg Jun 20 '12 at 13:44 -
@egreg I see this point, but still, the solution better allows user-based fine-tuning ;) – yo' Jun 20 '12 at 14:01
-
2
-
@nyuszika7h: I messed up when generating the image and forgot to use
\don the left-hand side, I guess. It shouldn't be italic in any case. – You Nov 25 '14 at 21:09
Presumable you are trying to both save on typing, and to exert some consistent notation throughout you article (good idea).
If you are making a macro for infinitesimals, you might as well make a marco for a derivative and an integral with limits.
Avoid single letter macros e.g. \d because they are often already defined.
\documentclass{article}
\usepackage{amsmath}
\usepackage{amsfonts}
\newcommand \dd[1] { \,\textrm d{#1} } % infintesimal
\newcommand \de[2] { \frac{\mathrm d{#1}}{\mathrm d{#2}} } % first order derivative
\newcommand \intl[4]{ \int\limits_{#1}^{#2}{#3}\dd{#4} } % integral with limits
\begin{document}
$$ \dd x=-\dd u $$
$$ y'=\de yx $$
$$ \intl0\infty{f(t)}t $$
\begin{align*}
\left(\intl{-\infty}\infty{e^{-x^2}}x\right)^2
&=\intl{-\infty}\infty{\intl{-\infty}\infty{e^{-(x^2+y^2)}}x}y \\
&=\intl0{2\pi}{\left(\left.-\frac{e^{-r^2}}2\right|_{r=0}^{r=\infty}\right)}\theta \\
&=\pi
\end{align*}
$$ V(x)=-\intl{\mathbb R^3}{}{\frac G{|x-y|}\rho(y)}{^3}y $$
\end{document}
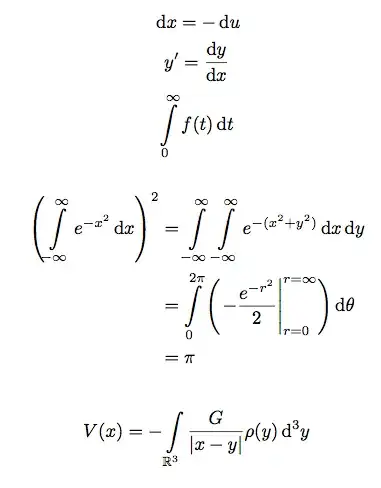
- 757,742
My answer is short, but it is surely an answer. So I post it here as an answer rather than a comment.
In my opinion, the letter "d" should be regarded as an operator rather than a variable when it is used to express the differential in mathematics. So the simplest way to realize this is to define a command via "\DeclareMathOperator{\td}{d}" in the whole document or to employ "\operatorname{d}" locally and occationally. Moreover, the command "\td" comes from "\textup{d}" in AmS-LaTeX.
See also the following comments at
and
- 146
-
This is wrong, sorry. Try
\td xto see what goes wrong (you got comments by LSpice telling the same). – egreg Sep 24 '23 at 07:46 -
There should be *no* space between “d” (upright or not) and the variable, but you always get a thin space. Look in every book on your shelf. – egreg Sep 24 '23 at 13:11
-
@egreg What's wrong? I used the command "\td" for many years and I didn't find any error. Please notice that *there should and must be some spaces in front of and behind any standard operator name*. Compare $x\sin x$, $x\operatorname{sin}x$, and $x\operatorname{d}x$. Is there any difference about the spaces in front of and behind these operators? Nothing, so they are all standard. – qifeng618 Sep 24 '23 at 13:31
-
One more word. In my opinion, we should do our best to use existed standard LaTeX commands as possible as we can, and we shouldn't manage to and try to construct our own specific LaTeX commands. By the way I have been using $\operatorname{e}^x$ and $\operatorname{i}$ to express the exponential function and the imaginary unit. – qifeng618 Sep 24 '23 at 13:40
-
You didn't look into your books, did you? The fact is that the differential “d” is not really a math operator like log or sin. – egreg Sep 24 '23 at 13:59
-
@egreg I read many mathematical books and noticed the special letter "d" for many years. To the best of my knowledge, there was no a standard format for the letter "d" in different mathematical books. Is there a standard format for the letter "d" in those books on your bookself? Which standard or format would you like me to obey? If you deny the differential "d" is a mathematical operator, what's it? Clearly not a variable yet. What's it? – qifeng618 Sep 24 '23 at 22:57
-
@egreg No matter what it is, I have just been typesetting it as an operator in my papers for many years. Many years ago, I didn't like the thin space behind the letter "d" as an operator and removed off the thin space by the command "!" or "!!", but now I don't adjust the thin space via "!" and I regard it as a full mathematical operator. In a word, there is no a standard format for the letter "d" in mathematical community, so I did according to my own understanding, seeing, and thinking for the beauty of mathematics. – qifeng618 Sep 24 '23 at 22:57
-
@egreg Please read the comment at the site https://mathoverflow.net/questions/455136/how-to-prove-negativity-of-a-3-times3-determinant-whose-elements-involve-triga#comment1178551_455136 – qifeng618 Sep 25 '23 at 04:06
As user69453 already said, I'd recommend you to use the Physics package.
Instead of using macros and dealing with spaces, you can just use \dd for the non-italic d. But, as barbara beeton stated, it's more important to write consistently than following a standard, which may not be used universally. Most of my college teachers (UPM, Spain) write the italic d for differentials.
Usage
Differential of x will be written as \dd{x}, while the nth differential of x would be \dd[n]{x}.
Example
\documentclass{article}
\usepackage{amsmath}
\usepackage{physics}
\begin{document}
\begin{align}
\biggl(\int_{-\infty}^\infty e^{-x^2}\dd{x}\biggr)^2
&= \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)}\dd{x}\dd{y} \
&= \int_0^{2\pi}\int_0^\infty e^{-r^2}r\dd{r}\dd{\theta} \
&= \int_0^{2\pi}\biggl(-{e^{-r^2}\over2}\bigg\vert_{r=0}^{r=\infty},\biggr)\dd{\theta}\
&= \pi \tag{q.e.d.}\
\end{align*}
%
[ V(\mathbf{x}) = -\int_{\mathbf{R}^3}
\frac{G}{|\mathbf{x}-\mathbf{y}|},\rho(\mathbf{y}),\dd[3]{\mathbf{y}} ]
\end{document}
Output
Advantages
The main advantages of using this solution:
- When using brackets, it chooses the ideal separation depending on neighbours. If you write it without brackets, for example
\dd x, there will be no separation. - By default, it follows the ISO 80000-2:2019 standard. However, you can add a package option to set italic as default style:
\usepackage[italicdiff]{physics}
Further Reading
-
This seems to be covered already in another answer; your additions are probably better-suited as a comment. – Werner Feb 02 '21 at 20:26
-
Sorry, but I disagree. The definition of
\ddis uselessly complicated and doesn't work as it should. – egreg Feb 02 '21 at 20:37 -
Thanks both, Werner and egreg. I agree with Werner, this should be a comment. However, I have little reputation for now and decided to make an answer as I can't comment. I thought it would be useful. Anyway, I apologise if it wasn't supposed to be like this. Should I delete the answer? Or maybe fix it? And, well... I didn't know that the definition of
\ddwas so complicated :( I don't want to start a chat here, so is there anyway you could explain me that out of here, egreg? Again, thank you! – Javiolonchelo Feb 02 '21 at 21:40

\mathrmor not depends on the traditions in your field. A thin space before the "d" in integrals is certainly required, Herbert's solution shows how to get it automatically (but using a macro for getting the "d"). – egreg Jun 20 '12 at 13:10amsmathmanual does not\rmit's integral d's: http://mirrors.ctan.org/macros/latex/required/amsmath/amsldoc.pdf – bers Mar 26 '19 at 16:18