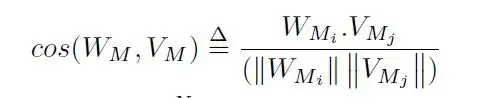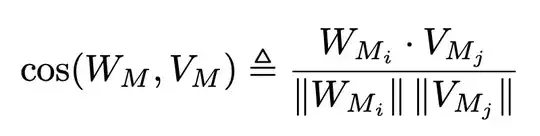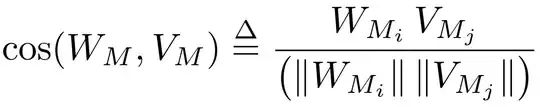Make the size of two resizable double vertical line (norm) operators uniform

Question

I want to put a double vertical line among some formulas in order to separate them, but the size is not the same. I used \left\| and \right\| for double vertical line. The size should follow the vertical line that encloses the WMi formula.

    {\textbf{cos(W_M, V_M)}\overset{\Delta}{=}\frac{W_{M_i}.V_{M_j}}{(\left\|W_{M_i} \right\|\left\|V_{M_j}\right\|)}}

Answer 1

Let's look at your input:

{\textbf{cos(W_M, V_M)}\overset{\Delta}{=}\frac{W_{M_i}.V_{M_j}}{(\left\|W_{M_i} \right\|\left\|V_{M_j}\right\|)}}

1. The outer braces do nothing at all, so it's best to remove them
2. \textbf just produces a warning and does nothing
3. “cos” should be \cos
4. \overset{\Delta}{=} is good, but probably you want \triangleq
5. The inner (or scalar) product should not be denoted by a (low) period, but rather with a centered dot
6. The parentheses (...) are not needed in the denominator and make for harder reading¹
7. \left and \right in your code do harm, rather than being helpful

Points 1–4 and 6 can be addressed very easily. For point 5, use \cdot.

Let's come to the main point of your question. For the norm of vectors, use

\lVert <vector> \rVert

It's generally not needed (nor advisable) to use \left\lVert and \right\rVert, because the automatically sized fences might be of different size or too tall anyway.²

Note, instead, \, between the two norms to help readers in distinguishing between them.³

\documentclass{article}
\usepackage{amsmath}
\usepackage{amssymb}
\begin{document}
\begin{equation}
\cos(W_M, V_M)
\triangleq
\frac{W_{M_i} \cdot V_{M_j}}{\lVert W_{M_i} \rVert,\lVert V_{M_j}\rVert}
\end{equation}
\end{document}

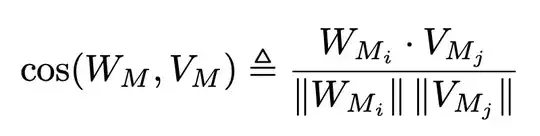
Footnotes

¹ With parentheses in the denominator, a reader might think that there's something missing. Avoid redundant parentheses.

² Here's what you get from adding \left and \right in front of \lVert and \rVert

Can you see the difference, which is caused by the fact that “j” descends below the baseline? There is no need that the fences completely cover what's between them, particularly if it's just a descender or an accent that's not covered.

³ Without \, the output would be

which requires the reader to count the bars.

Answer 2

Don't use \left...\right unless it's really necessary. Use fixed-height adjustments like \bigl...\bigr. If you must, you can use \vphantom to adjust the \left...\right delimiters to be equal (\left\| \vphantom{V_{M_j}} W_{M_i} \right\|). Below I suggest dropping the sizing you used.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
[
  \cos(W_M, V_M) \overset{\Delta}{=}
    \frac{W_{M_i} , V_{M_j}}{\bigl( | W_{M_i} | , | V_{M_j} | \bigr)}
]
\end{document}

Answer 3

With use of the mathtools and amssymb packages:

\documentclass{article}
\usepackage{mathtools, amssymb} 
\DeclarePairedDelimiter{\norm}{\lVert}{\rVert}
\begin{document}
[
  \cos(W_M, V_M) \triangleq
    \frac{W_{M_i} , V_{M_j}}
         {\bigl(\norm{W_{M_i}} \norm{V_{M_j}}\bigr)}
]
or 
[
  \cos(W_M, V_M) \triangleq
    \frac{W_{M_i} , V_{M_j}}
         {\bigl(\norm{W_{M_{i\vphantom{j}}}} \norm{V_{M_j}}\bigr)}
]
\end{document}