UPDATE
I asked the author of 3dtools at here. With new update, now you can construct the points S without using the Maple.
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,decorations.pathreplacing,3dtools} % https://github.com/marmotghost/tikz-3dtools
\begin{document}
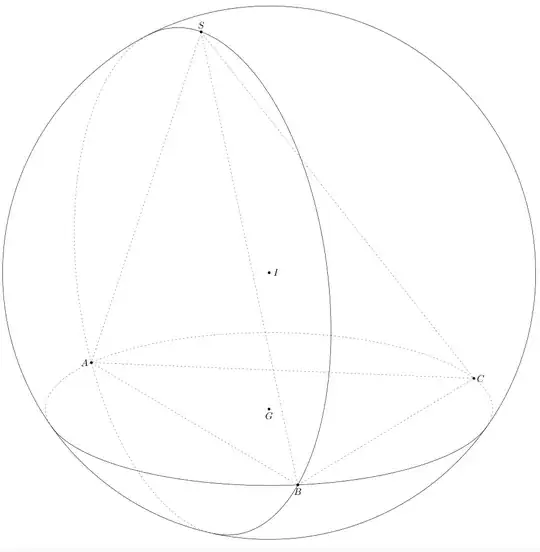
\begin{tikzpicture}[line cap=round,line join=round,c/.style={circle,fill,inner sep=1pt},
declare function={lAB=15;lAC=14;lBC=13;lAD=16;lBD=17;lCD=18;}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=60,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos(-1*(lBC*lBC-lAC*lAC-lAB*lAB)/(2*lAB*lAC))}
\path (0,0,0) coordinate (A)
(lAB,0,0) coordinate (B)
({lAC*cos(\mytheta)},{lAC*sin(\mytheta)},0) coordinate (C);
\path[overlay,3d/aux keys/i1=S,3d/aux keys/i2=D',
3d/intersection of three spheres={rA=lAD,rB=lBD,rC=lCD}];
\path[3d/circumsphere center={A={(A)},B={(B)},C={(C)},D={(S)}}]
coordinate (I);
\pgfmathsetmacro{\myR}{sqrt(TD("(I)-(A)o(I)-(A)"))} ;
\path[3d/circumcircle center={A={(A)},B={(B)},C={(C)}}] coordinate (G);
\draw[3d/screen coords] (I) circle[radius=\myR];
\path pic{3d/circle on sphere={R=\myR,C={(I)}, P={(G)}}};
\path[3d/circumcircle center={A={(A)},B={(B)},C={(S)}}] coordinate (T);
\path pic{3d/circle on sphere={R=\myR,C={(I)}, P={(T)}}};
\path foreach \p/\g in {A/180,B/-90,C/0,S/90,G/-90,I/0}{(\p)node[c]{}+(\g:2.5mm) node{$\p$}};
\draw[3d/hidden] (A) -- (C) (S) -- (A) (S) -- (B) (S) --(C) (A) -- (B) -- (C);
\end{scope}
\end{tikzpicture}
\end{document}
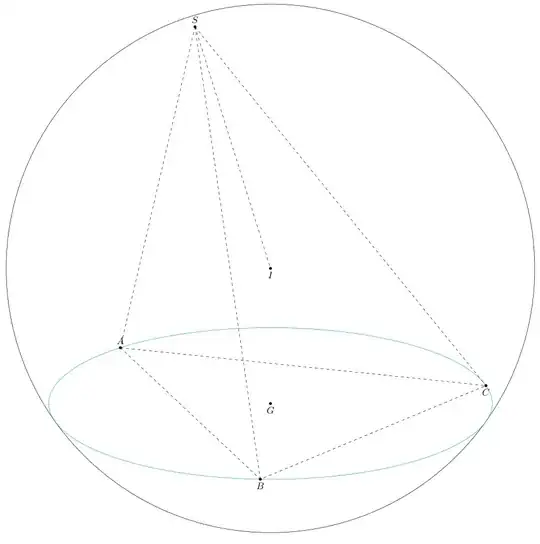
I use Maple to find the coordinates of the point S.


\documentclass[border=3.14mm]{standalone}
\usepackage{tikz,tikz-3dplot}
\usetikzlibrary{fpu}
\def\pgfmathsetmacroFPU#1#2{\begingroup%
\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\pgfmathsetmacro{#1}{#2}%
\pgfmathsmuggle#1\endgroup}%
\begin{document}
\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords]
\begin{scope}[/pgf/fpu,/pgf/fpu/output format=fixed]
\path
(0,0,0) coordinate (A) node[above]{$A$}
(15,0,0) coordinate (B) node[below]{$B$}
(42/5, 56/5,0) coordinate (C) node[below]{$C$}
(32/5, 32/55,{(16*sqrt(41))/7}) coordinate (S) node[above]{$S$}
(32/5, 32/55,{(-16*sqrt(41))/7}) coordinate (S') node[below]{$S'$}
(15/2, 25/8,{(135*sqrt(41))/164}) coordinate (I) node[below]{$I$}
(15/2, 25/8,0) coordinate (G) node[below]{$G$};
;
\pgfmathsetmacroFPU{\myR}{(5*sqrt(403645))/328}
\draw[tdplot_screen_coords] (I) circle [radius = \myR];
\pgfmathsetmacroFPU{\myr}{65/8};
\draw[cyan] (G) circle [radius = \myr];
\end{scope}
\draw [dashed] (A) -- (C) (S) --(I) (S) -- (A) (S) -- (B) (S) -- (C) (A) -- (B) -- (C);
\foreach \X in {A,B,C,S,S',I,G} \fill (\X) circle (1.5pt);
\end{tikzpicture}
\end{document}
You can use \usetikzlibrary{3dtools} here
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},line cap=butt,
line join=round]
\path
(0,0,0) coordinate (A) node[above]{$A$}
(15,0,0) coordinate (B) node[below]{$B$}
(42/5, 56/5,0) coordinate (C) node[below]{$C$}
(32/5, 32/55,{(16*sqrt(41))/7}) coordinate (S) node[above]{$S$};
\path[3d/circumsphere center={A={(A)},B={(B)},C={(C)},D={(S)}}]
coordinate (I) node[above]{$I$};
\pgfmathsetmacro{\myR}{sqrt(TD("(I)-(A)o(I)-(A)"))} ;
\path[3d/circumcircle center={A={(A)},B={(B)},C={(C)}}] coordinate (G);
\draw[red, 3d/screen coords] (I) circle[radius=\myR];
\path pic[blue]{3d/circle on sphere={R=\myR,C={(I)}, P={(G)}}};
\draw[3d/hidden] (A) -- (B) -- (C) --cycle (B) -- (I)
(S) --(A) (S) --(B) (S)--(C);
\foreach \X in {A,B,C,I,S} \fill (\X) circle (1.5pt)
;
\end{tikzpicture}
\end{document}






