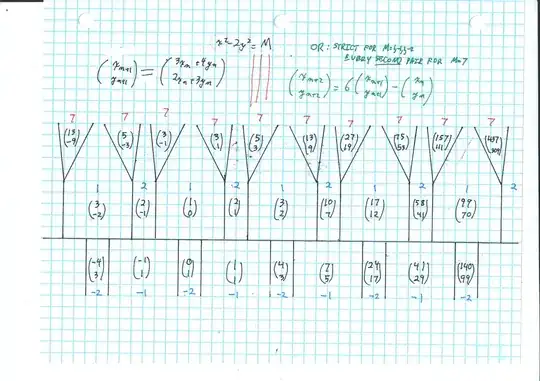
How can I find the integer solutions of the generalized Pell equation $x^2-2y^2=49$
I have an algorithm, but this only works if $D\ge r^2+\frac{\left(|r|+1\right)}2$, (where $x^2-Dy^2=r^2$).
The problem is we've covered Pell equation and elementary number theory a couple of weeks ago, since then we're doing some algebraic number theory, but I cannot find any useful theorems there.
One solution by guessing is $(r,s)=(11,6)$ and the minimal solution to $x^2-2y^2=1$ is $(t,u)=(3,2)$ and then a second solution can be found $(x,y)=(rt+Dsu,ru+st)=(57,40)\dots$, but these are not all, am I wrong ?