Anyone can help solve th following? $\left( {\begin{array}{*{20}{c}} {2n} \\ n \end{array}} \right)$ means $2n$ chooses $n$. Thanks!
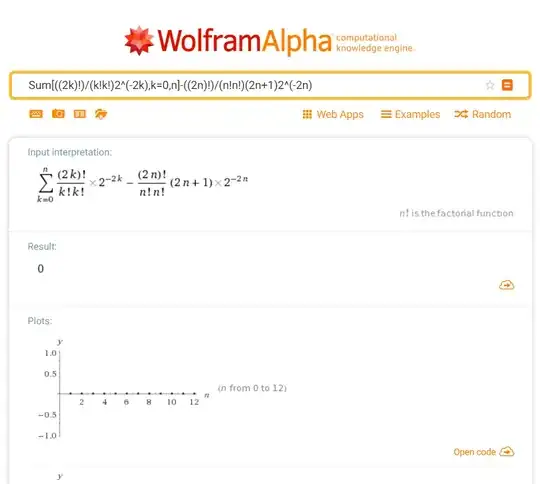
$\sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}{c}} {2k} \\ k \end{array}} \right){2^{ - 2k}}} = \sum\limits_{k = 0}^n {\frac{{(2k)!}}{{k!k!}}{2^{ - 2k}}} = \frac{{(2n)!}}{{n!n!}}(2n + 1){2^{ - 2n}} = \left( {\begin{array}{*{20}{c}} {2n} \\ n \end{array}} \right){2^{ - 2n}}(2n + 1)$
The report from wolframalpha shows they indeed equal.
How about induction? The base case $n = 0$ is easily verified. Then
\begin{align} \binom{2n}{n}2^{-2n}(2n+1) + \binom{2n+2}{n+1}2^{-2n-2} &= \binom{2n+2}{n+1}2^{-2n-2}\biggl[\frac{4(n+1)^2}{2n+2} + 1\biggr] \\ &= \binom{2n+2}{n+1}2^{-2n-2}\bigl(2n+2+1\bigr) \end{align}
is the induction step.
I tried to get a bijection but it seems kind of complicated, i will definitely be interested if someone has a bijection for it. Using generation functions is easy tho.
Just noticing that the LHS is a convolution of central binomial coefficients and powers of $4$ and so $$\sum _{k = 0}^n\binom{2k}{k}2^{2n-2k}=[x^n]\frac{1}{\sqrt{1-4x}}\frac{1}{1-4x}=[x^n](\frac{1}{\sqrt{1-4x}}+\frac{4x}{\sqrt{1-4x}^3})=([x^n]\frac{1}{\sqrt{1-4x}}+[x^n]\frac{4x}{\sqrt{1-4x}^3})=\binom{2n}{n}+2n\binom{2n}{n},$$
where the last step is just noticing that $(\frac{1}{\sqrt{1-4x}})'=\frac{2}{\sqrt{1-4x}^3}.$
My approach to a bijection is noticing that $\binom{[2k]}{k}2^{2n-2k}$ can be realized as a path from $(0,0)$ to $(k,k)$ plus a path that can be reached outside or inside the $n\times n$ box. I will add more details soon.
