For the Fibonacci numbers, show for all $n$: $F_1^2+F_2^2+\dots+F_n^2=F_nF_{n+1}$

Question

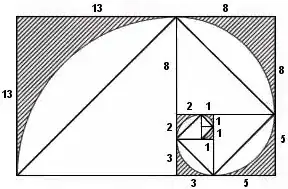
The definition of a Fibonacci number is as follows:

$$F_0=0\\F_1=1\\F_n=F_{n-1}+F_{n-2}\text{ for } n\geq 2$$

Prove the given property of the Fibonacci numbers for all n greater than or equal to 1. $$F_1^2+F_2^2+\dots+F_n^2=F_nF_{n+1}$$

I am pretty sure I should use weak induction to solve this. My professor got me used to solving it in the following format, which I would like to use because it help me map everything out...

This is what I have so far:

Base Case: Solve for $F_0$ and $F_1$ for the following function: $F_nF_{n+1}$.

Inductive Hypothesis: What I need to show: I need to show $F_{n+1}F_{n+1+1}$ will satisfy the given property. Proof Proper: (didn't get to it yet)

Any intro. tips and pointers?

Answer 1

This identity is clear from the following diagram:

(imagine here a generalized picture with $F_i$ notation)

The area of the rectangle is obviously

$$F_n(F_{n}+F_{n-1})=F_nF_{n+1}$$

On the other hand, since the area of a square is x^2, it is obviously:

$$F_1^2+F_2^2+\dots+F_n^2$$

Therefore:

$$F_1^2+F_2^2+\dots+F_n^2=F_nF_{n+1}$$

---

You can even convert this graphical proof to an inductive proof - your inductive step would consist of adding a square $F_{n+1} * F_{n+1}$.

Answer 2

The inductive assumption for $n$ is

$$F(1)^2+\ldots+F(n)^2=F(n)F(n+1)$$.

Using this, the $n+1$ case is:

$$\begin{align*} F(1)^2+\ldots +F(n)^2+F(n+1)^2 &=F(n)F(n+1)+F(n+1)^2 \\ &=F(n+1)(F(n)+F(n+1)) \\ &=F(n+1)F(n+2)\end{align*} $$

Answer 3

A nice pictorial proof can be obtained by first placing two 1x1 squares horizontally (so that's $F_1+F_2$ so far), then a 2x2 square on top of those (so now we have a 2x3 rectangle containing $F_1^2,F_2^2,F_3^2$), then a 3x3 rectangle to the right of the rectangle we now have (so now it has size 3x5), and so on. After placing the $n$th square in this diagram, the rectangle will have dimensions $F_n \times F_{n+1}$, and the total number of unit squares inside it will be the sum of the squares of the first $n$ Fibonacci numbers.

Answer 4

Following can be another way:

$$F_rF_{r+1}=F_r(F_r+F_{r-1})=F_r^2+F_{r-1}F_r$$

Putting $r=1,2,3,\cdots,n-1,n$ and adding we get

$$F_nF_{n+1}=\sum_{1\le r\le n }F_r^2+F_0F_1=\sum_{1\le r\le n }F_r^2$$ as $F_0=0$

Answer 5

Since $F_k=F_{k+1}-F_{k-1}$ for all $k\geq 1$, we have that $$\sum_{k=1}^n F_k^2=\sum_{k=1}^n F_k(F_{k+1}-F_{k-1})$$ $$\implies\sum_{k=1}^n F_k^2=\sum_{k=1}^n F_kF_{k+1}-\sum_{k=1}^n F_kF_{k-1}$$ But since $F_0=0$, we have $S=\sum_{k=1}^n F_kF_{k-1}=\sum_{k=1}^{n-1} F_{k+1}F_{k}$. Then $\sum_{k=1}^n F_kF_{k+1}=S+F_nF_{n+1}$ and finally we get, $$\sum_{k=1}^n F_k^2=F_nF_{n+1}$$