Suppose I start with $x_0$, a normalized vector in $d$ dimensions, and get $x_{i+1}$ by moving in a random direction on surface of sphere. What is expected number of steps until I first see $\langle x_0, x_k\rangle<0$?
More precisely, suppose entries of $z_i$ are standard normal normalized to have $E[\|z\|^2]=s$, and we have
$$\hat{x}_{i+1}=x_i+z_i$$
$$x_{i+1}=\hat{x}_{i+1}/\|\hat{x}_{i+1}\|$$

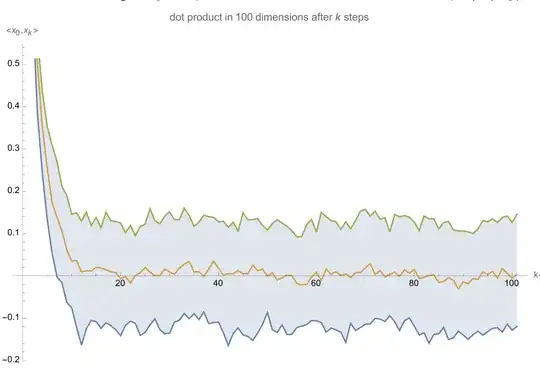
For instance, in $d=100$, $s=1$ distribution of dot products of $x_k$ and $x_0$ looks like this:
This value indicates how long it takes to "forget" which side of the plane you started on, and I want to know if there's a simple dependence of "time to forget" on $d$ and $s$. For instance in simulation above with $d=100,s=1$ it's somewhere between 5 and 20
Motivation:
This would give a way to prove of "triangle equality for cosines" which is needed for a different application (background)