Show that a simple inequality holds: $a

Question

I'm trying to show that $\dfrac{a}{b} < \dfrac{a + 1}{b + 1}$ given $a < b$ and $b$ is positive.

Ideas?

Answer 1

Consider the difference

$$\frac{a + 1}{b + 1} - \frac{a}{b} = \frac{(a + 1)b - a(b + 1)}{b(b + 1)} = \frac{b - a}{b(b + 1)} > 0$$

Answer 2

Here is a geometrical explanation in terms of slopes.

If take $b$ for abscissa and $a$ as ordinate of a certain point $M$, adding vector $\binom{1}{1}$ to vector $\vec{OM}=\binom{b}{a}$ will an increase of the slope (due to the fact that $a>b$) as illustrated on the following figure: 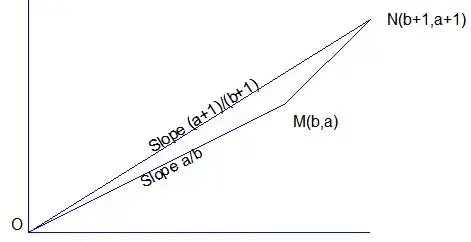Fig. 1: $(a+1)/(b+1) > a/b$ is equivalent to the fact that slope $ON$ > slope $OM$.

Remark: moreover the signed area of triangle $OMN$ is the half of $\det(\vec{OM},\vec{ON})$ (in correspondence with $\vec{OM} \times \vec{ON}$.

Answer 3

Remember that you have the identity $\dfrac ab=\dfrac cd$ then it is also equal to $\dfrac{a+c}{b+d}$.

This can be extended to inequalities as well (assuming positive denominators) $\dfrac ab<\dfrac cd$ then $\dfrac ab<\dfrac{a+c}{b+d}$.

$\dfrac{a+c}{b+d}-\dfrac ab=\dfrac{ab+bc-ab-ad}{b(b+d)}=\dfrac{\overbrace{bc-ad}^{>0\ (*)}}{\underbrace{b(b+d)}_{>0\ (**)}}>0$

• (*) from hypothesis $\frac ab<\frac cd$
• (**) from hypothesis of positive denominators

Here this is an application:

$a<b\ ,\ b>0\implies \dfrac ab<\dfrac 11\small{\text{ [with >0 denominators]}}\implies \dfrac ab<\dfrac{a+1}{b+1}$

Answer 4

There is a more general and expressive result:

Let $a,b, h$ be numbers ($b,h>0$).

• If $\dfrac ab<1$, then $\;\dfrac ab<\dfrac{a+h}{b+h}<1$.

• If $\dfrac ab>1$, then $\;\dfrac ab>\dfrac{a+h}{b+h}>1$.

To prove it, as the denominators are positive, you just have to compare the cross-products: $$\frac ab<\dfrac{a+h}{b+h}\iff a(\not\mkern-2mu b+h)<b(\not\mkern-2mu a+h)\iff ah<bh\iff\frac{a\not h}{b\not h}<1$$ Similar verification for the other inequalities.