10

I have undirected weighted labeled graph. How i can generate and visualize tree graph, showing me all simple paths (and dead ends) from vertice A to vertice B? For example, for this graph

this graph

to show all simple paths with dead ends between vertices 1 and 2 i need to generate such tree

such tree

Alex78191
  • 203
  • 1
  • 5

4 Answers4

5

How i can generate and visualize tree graph, showing me all simple paths (and deadlocks) from vertice A to vertice B?

This answer has a brute force solution and I have not tested it extensively. At least the visualization of the result tree graph should be useful.

Creating the graph

graphRules = {1 <-> 2, 1 <-> 4, 1 <-> 5, 2 <-> 3, 3 <-> 4, 3 <-> 5, 
   4 <-> 5};
gr = Graph[graphRules, VertexLabels -> "Name"]

enter image description here

Paths

First we find all the paths from v1to v2:

{v1, v2} = {1, 2};

paths = FindPath[gr, v1, v2, Length[VertexList[gr]], All]

(* {{1, 2}, {1, 5, 3, 2}, {1, 4, 3, 2}, {1, 5, 4, 3, 2}, {1, 4, 5, 3, 2}} *)

Deadlock paths

The deadlock paths -- as defined here as locking of resources -- are found with brute force.

1. Find all inner veritces in the v1-to-v2 paths:

innerVertices = Complement[Flatten[paths], {v1, v2}]

(* {3, 4, 5} *)

2. Find all paths from the inner vertices to v2:

innerVerticesPaths = 
 Map[# -> FindPath[gr, #, v2, Length[VertexList[gr]], All] &, innerVertices];

3. For each path $p$ of the v1-to-v2 paths we select inner vertices paths $iv(p)$ that would produce deadlock paths if concatenated with $p$. This is done with the help of the following functions:

Clear[PickDeadlockPaths]
PickDeadlockPaths[headPath_, tailPaths_] :=  
  Block[{v = headPath[[-1]], ivs},
    ivs = headPath[[1 ;; -2]];
    If[Length[ivs] == 0, {},
     Union@
      Cases[tailPaths, {v, x___, d : (Alternatives @@ ivs), y___} :> {v, x, d}]
     ]
    ] /; Apply[And, Map[headPath[[-1]] == First[#] &, tailPaths]];
PickDeadlockPaths[___] := {};

Clear[MakeDeadlockPaths]
MakeDeadlockPaths[headPath_] :=
  Block[{dps},
   dps = PickDeadlockPaths[headPath, headPath[[-1]] /. innerVerticesPaths];
   If[Length[dps] == 0, {},
    Map[Join[headPath, Rest[#]] &, dps]
   ]
  ];

4. Here is the deadlock paths finding:

allDeadlockPaths = 
  Flatten[Map[
    Join @@ Table[MakeDeadlockPaths@Take[#, {1, i}], {i, 2, Length[#] - 1}] &,
     Select[paths, Length[#] > 2 &]], 1];

allDeadlockPaths = Union[Most /@ allDeadlockPaths]

(* {{1, 4}, {1, 5}, {1, 4, 3}, {1, 4, 5}, {1, 5, 3}, {1, 5, 4}, {1, 4, 3, 5}, {1, 4, 5, 3}, {1, 5, 3, 4}, {1, 5, 4, 3}} *)

Tree with all paths

Using the package TriesWithFrequencies.m we plot the requested tree:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/TriesWithFrequencies.m"]

ptrie = TrieCreate[Join[paths, allDeadlockPaths]][[2]];
TrieForm[ptrie]

enter image description here

The first element in each tree node corresponds to a graph vertiex, the second element is a traversal frequency.

(The package TriesWithFrequencies.m is described in this blog post "Tries with frequencies for data mining".)

Anton Antonov
  • 37,787
  • 3
  • 100
  • 178
  • Thanks Anton, +1. The TriesWithFrequencies.m package looks great. I will definitely use this in the future. I have actually be trying to define frequency trie structures for use with the Front-End argument string completion feature 113116. – Rashid May 22 '16 at 02:50
  • @Rashid Thanks. You might also want to look into this document: "Tries.pdf", which has more extensive examples for that package. – Anton Antonov May 22 '16 at 02:57
  • I am having a problem opening the Github Tries.pdf link. My browser keeps crashing while the Github page tries to render the PDF (presumably using PDF.js). Have you ever run into this problem? Do you know of any work arounds? (If not, I could just download the file, but figured I would ask as others may run into the same problem.) – Rashid May 22 '16 at 15:19
  • Sorry, no -- it works fine for me. – Anton Antonov May 22 '16 at 16:32
4

@AntonAntonov's answer with the TriesWithFrequencies.m package is more elegant and useful, but here is a brute force approach without any extra packages.

(Note: This approach finds all simple paths including dead ends, see comments for more details. Edited to process more general graphs with more than 10 vertices.)

The main challenge is that the final tree should have the same graph vertices and edges depicted in different positions based on path order. One way to get around this problem is to relabel the vertices as we construct paths, and then use the VertexLabels function to relabel the vertices at the end.

Step 1 - Define the undirected graph

Edit: introduced maxVertexValue here to make subsequent code applicable to larger graphs

exampleGraph =  Graph[{1 <-> 2, 1 <-> 4, 1 <-> 5, 2 <-> 3, 3 <-> 4, 3 <-> 5, 4 <-> 5}, VertexLabels -> "Name"]
maxVertexValue = Max[VertexList[exampleGraph]];

enter image description here

Step 2 - UseFindPath to construct a list of all relevant paths. This include the paths that successfully get from "1" to "2" as well as the lists that start from "1" but do not contain "2". 

successfulPaths = FindPath[exampleGraph, 1, 2, 5, All];
unsuccessfulPaths =  Flatten[Table[Select[FindPath[exampleGraph, 1, x, maxVertexValue, All],!MemberQ[#, 2] &], {x, 3, maxVertexValue}], 1]
allPaths = Join[successfulPaths, unsuccessfulPaths];

Or more concisely:

allPaths = Flatten[Table[Select[FindPath[exampleGraph, 1, x, maxVertexValue, All], Last[#] == 2 || ! MemberQ[#, 2] &], {x, 2, maxVertexValue}],1];

Either case returns the following allPaths list: 

{{1, 2}, {1, 5, 3, 2}, {1, 4, 3, 2}, {1, 5, 4, 3, 2}, {1, 4, 5, 3, 2}, {1, 5, 3}, {1, 4, 3}, {1, 5, 4, 3}, {1, 4, 5, 3}, {1, 4}, {1, 5, 4}, {1, 5, 3, 4}, {1, 5}, {1, 4, 5}, {1, 4, 3, 5}}

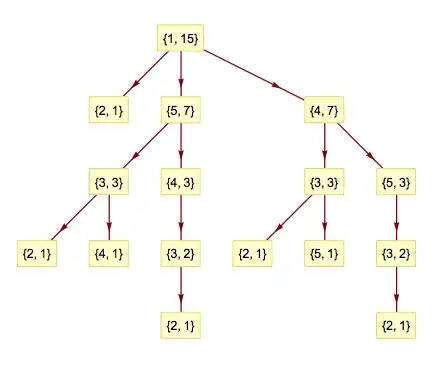
Step 3 - Give every vertix a path dependent name (EDITED to label each vertex with a path list). For example, the path list {1,5,3,2} can be relabeled as {{1},{1,5},{1,5,3},{1,5,3,2}}. These labels will help us group all 1->5 paths in the first step together. 

relabeldPaths = Table[x[[1 ;; y]]], {x, allPaths}, {y, Length[x]}];

Step 4 - Convert the relabeled paths list to a unique set of directed edges and vertices. There is probably a much better way to do this, but I combined EdgeList with PathGraph as follows:

pathEdges = Flatten[Map[EdgeList[PathGraph[#, DirectedEdges -> True]] &, relabeldPaths] /. DirectedEdge -> Rule];
treeEdges = DeleteDuplicates[pathEdges];
treeVertices = VertexList[Graph[treeEdges]];

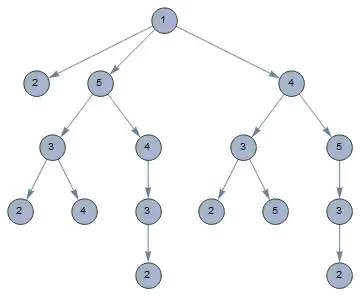
Step 5 - Plot final graph using VertexLabels to select the Last part of each vertex name. (EDITED to make labels clearer)

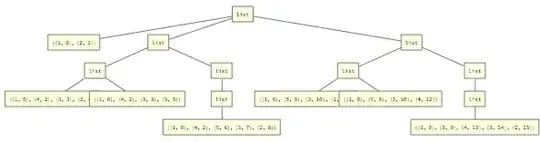
Graph[treeEdges, VertexSize -> Large, VertexLabels -> Table[x -> Placed[Last[x], Center], {x, treeVertices}], ImageSize -> Medium]

enter image description here

EDIT: Here is a generalized module for this approach for quick copy/paste

pathTreeGraph[graph_, startingVertex_, endingVertex_] := 
 Module[{maxVertexValue, allPaths, relabeldPaths, pathEdges, 
   treeEdges, treeVertices}, maxVertexValue = Max[VertexList[graph]];
  allPaths = Flatten[Table[
     Select[FindPath[graph, startingVertex, x, maxVertexValue, All],           
     Last[#] == endingVertex || !MemberQ[#, endingVertex] &], 
     {x, DeleteCases[VertexList[graph], startingVertex]}], 1];
  relabeldPaths = Table[Flatten[x[[1 ;; y]]], {x, allPaths}, {y, Length[x]}];
  pathEdges = Flatten[Map[EdgeList[PathGraph[#, DirectedEdges -> True]] &, relabeldPaths] /. DirectedEdge -> Rule];
  treeEdges = DeleteDuplicates[pathEdges];
  treeVertices = VertexList[Graph[treeEdges]];
  Graph[treeEdges, VertexSize -> Large, 
   VertexLabels -> Table[x -> Placed[Last[x], Center], {x, treeVertices}], 
   ImageSize -> Medium]]

exampleGraph = Graph[{1 <-> 2, 1 <-> 4, 1 <-> 5, 2 <-> 3, 3 <-> 4, 3 <-> 5, 4 <-> 5}, VertexLabels -> "Name"]
pathTreeGraph[exampleGraph, 1, 2]

UPDATE: Example with more than 10 vertices

ButterflyGraph[2, VertexLabels -> "Name", ImageSize -> Medium]
pathTreeGraph[ButterflyGraph[2], 1, 2]

enter image description here enter image description here

Rashid
  • 1,523
  • 10
  • 18
  • This answer does not find the deadlock paths. For example, for this graph Graph[{1 <-> 2, 1 <-> 4, 1 <-> 5, 2 <-> 3, 3 <-> 4, 3 <-> 5, 4 <-> 5, 4 <-> 6}] it will show the path {1,4,6} which is not a deadlock path. – Anton Antonov May 22 '16 at 12:05
  • On a separate note, I do like the tree of paths visualization approach. – Anton Antonov May 22 '16 at 12:07
  • @AntonAntonov, thanks for the help. I guess I don't understand what a deadlock is, because I would have thought that {1,4,6} was a deadlock since it ends in an isolated vertex (6). Here is the graph and the resulting tree that my code produces. Do you know of any sites that might provide a nice definition of a deadlock path? (I tried searching online, but couldn't find anything that was very helpful with regard to deadlock paths and graphs.) Sorry, I am new to graphs, but am trying to use Mathematica to help me learn. – Rashid May 22 '16 at 12:48
  • 1
    You are raising a valid concern -- I think we need to ask OP do provide a definition of deadlock paths. I am referring to this one: https://en.wikipedia.org/wiki/Wait-for_graph . – Anton Antonov May 22 '16 at 13:10
  • Thanks @AntonAntonov, I appreciate the help! I will also ask the OP above. – Rashid May 22 '16 at 13:20
  • The OP does consider {1,4,6} of the graph I mentioned to be a "deadlock path". (And in my answer I do not.) So your answer works for OP's question. – Anton Antonov May 22 '16 at 14:56
  • Thanks @AntonAntonov. In any case, I still prefer your answer and will definitely use your TriesWithFrequency.m package in the future for other projects. Thanks for helping me learn about this stuff. – Rashid May 22 '16 at 15:11
  • Dead end (deadlock as was writed before) is vertice that have no neighbor vertices that have not been visited yet in path. All neighbours of the vertice were already visited in path. – Alex78191 May 22 '16 at 16:12
  • @Rashid You can alter the algorithm for graphs with number of nodes greater or equal to 10. – Alex78191 May 22 '16 at 18:26
  • @Alex78191, I have updated my answer to use path-dependent lists for each vertex (rather than strings). This also it to handle graphs with more than 10 vertices. I also cleaned up the label displays. Hope this helps. – Rashid May 22 '16 at 20:33
2

Okay, I knew I was on to something but I didn't quite pull it together the first time. Here is a second attempt, still probably not as clean as it should be, and not entirely general, but I think at least delivering on the promise of a recursive solution.

rls = {1 -> 2, 1 -> 4, 1 -> 5, 2 -> 3, 3 -> 4, 3 -> 5, 4 -> 5};
asc = GroupBy[Join @@ Permutations /@ rls, First -> Last];

f[r_, t_] := f[1][r, t]

f[i_][n___, r_, t_] := 
  Complement[r /. asc, {n, r}] //
   {n, r}[[i]] @@ 
     If[# === {}, r, f[i + 1][n, r, #, t] & /@ #] &

f[i_][n___, t_, t_] := t

f[1, 2] // TreeForm

enter image description here

Useful related questions:

Old answer

An idea:

rls = {1 -> 2, 1 -> 4, 1 -> 5, 2 -> 3, 3 -> 4, 3 -> 5, 4 -> 5};
asc = GroupBy[Join @@ Permutations /@ rls, First -> Last];

ClearAll[f]

f[n___, r_, t_] :=
  Complement[r /. asc, {n, r}] //
    If[# === {}, 〈n, r〉, f[n, r, #, t] & /@ #] &

f[n___, t_, t_] := 〈n, t〉

out = f[1, 2]

{〈1, 2〉, {{〈1, 4, 3, 2〉, 〈1, 4, 3, 5〉},
 {{〈1, 4, 5, 3, 2〉}}}, {{〈1, 5, 3, 2〉, 〈1, 5, 3, 4〉},
 {{〈1, 5, 4, 3, 2〉}}}}

I am trying to think of a nice way to visualize this. For the time being I'll borrow ideas from Rashid's answer:

out = Flatten[out] /. AngleBracket -> List;

BooleanGraph[Or,
  Sequence @@ (PathGraph @ Rest @ FoldList[Append, {}, #] & /@ out),
  VertexShapeFunction -> ({Disk[#, 0.2], White, Text[Last @ #2 ~Style~ 20, #]} &)
]

enter image description here

Community
  • 1
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
1

Here's a relatively simple recursive solution, with explanation:

g = Graph[{1, 2, 3, 4, 5}, {1 \[UndirectedEdge] 2, 
   2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 5, 
   1 \[UndirectedEdge] 5, 1 \[UndirectedEdge] 4, 
   3 \[UndirectedEdge] 4, 4 \[UndirectedEdge] 5}]

Start and end points:

s = 1;
t = 2;

Recursive descent:

f[soFar_] :=
 With[
    {current = soFar[[-1, 1]]},
    {unvisited = Complement[AdjacencyList[g, current], soFar[[All, 1]]]},
    If[current === t || unvisited === {},
     soFar,
     f@Append[soFar, {#, k++}] & /@ list @@ unvisited
   ]
 ]

Explanation:

  • soFar is the vertices in the path so far
  • current is the current node we are visiting. We will try to move on to all neighbours of current if they were not yet visited (see AdjacencyList)
  • If we reach the target t, we stop with the recursion. If there are no unvisited neighbours, we stop with the recursion.
  • k is an extra label used to distinguish between events of encountering the same node through different paths.
  • list is just a distinct head which we will flatten out later, without touching other parts of the expression.

PathGraph chokes on vertex names that are lists, so we make our own ...

pathGraph[vertices_] := 
 Graph[DirectedEdge @@@ Partition[vertices, 2, 1]]

Compute all paths and merge them into a tree.

k = 0; 
GraphUnion @@ pathGraph /@ Flatten[f[{{s, k++}}], Infinity, list]

Labels vertices with their original name (i.e. do not display the value of k).

Graph[%, VertexLabels -> {{a_, b_} :> a}]

Mathematica graphics

To better understand how f works, try this:

k = 0;
f[{{s, k++}}]

% /. e : Except[_list] :> ToString[e] // TreeForm

Mathematica graphics

This expression tree reflects the structure of the tree we are building. The displayed leaf names are the paths used to get to that leaf.

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263