Method starts off by replacing all heads in the expression with the appropriate node index, then deduces the edge list by parsing the substituted node-index-expression. Note that input expression must be wrapped in Hold (or HoldComplete) to prevent evaluation of e.g. Plus[1, 2] into 3.
(* sow node -> label replacements *)
sowLabel[x_?AtomQ] := (Sow[# -> x]; #) &[c++];
sowLabel[x_] := x;
(* sow parent -> child replacements *)
sowEdge[head_[arg__]] := (Sow[head -> #] & /@ {arg}; head);
sowEdge[x_?AtomQ] := x;
(* the expression to be parsed into a tree *)
expr = Hold[Log[Sin[1 + 2], ToExpression["1" <> "0"]]];
FullForm@expr
Hold[Log[Sin[Plus[1, 2]], ToExpression[StringJoin["1", "0"]]]]
(* replace heads with node index & collect index -> label list *)
c = 1;
{new, labels} = Reap@ReleaseHold@Map[sowLabel, expr, {2, \[Infinity]}, Heads -> True]
{
1[2[3[4, 5]], 6[7[8, 9]]],
{{1 -> Log, 2 -> Sin, 3 -> Plus, 4 -> 1, 5 -> 2, 6 -> ToExpression, 7 -> StringJoin, 8 -> "1", 9 -> "0"}}
}
(* create graph edges from substituted expression *)
edges = Sort@Most@First@Last@Reap@Map[sowEdge, {new}, {0, \[Infinity]}]
{1 -> 2, 1 -> 6, 2 -> 3, 3 -> 4, 3 -> 5, 6 -> 7, 7 -> 8, 7 -> 9}
(* plot results *)
{
TreeGraph[edges,
VertexLabels -> First@labels, ImagePadding -> {{1, 35}, {0, 10}}
],
LayeredGraphPlot[edges,
VertexLabeling -> True,
VertexRenderingFunction :> (Inset[
Framed[InputForm[#2 /. First@labels], Background -> Hue[.15, .3, 1]], #1] &)
],
TreeForm[expr, ImageSize -> 230]
}
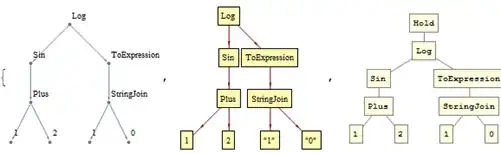
Hold[Log[Sin[Plus[1, 2]], ToExpression[StringJoin["1", "0"]]]]
Note, that TreeForm keeps the Hold wrapper.

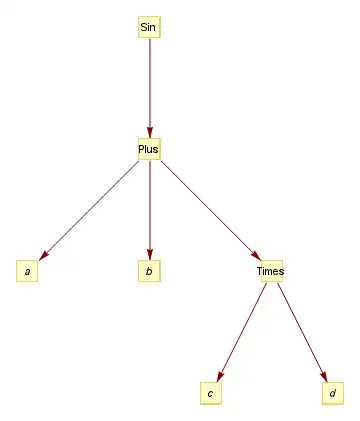
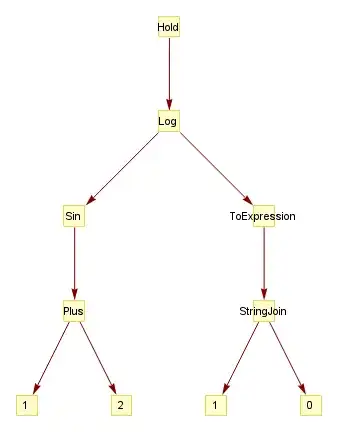
TreeFormproduces just graphics. Output ofTreeGraphgives aGraphobject which carries complete information about graph and can be computed with. – Vitaliy Kaurov Oct 03 '12 at 08:57