How to connect some separate components with shortest total length line

Question

Maybe this question is too hard. So I try to make a simple version to research.

Simulating a simple graph than that post.

SeedRandom[2]
p = RandomReal[1, {20, 2}];
sortPoint[p_] := 
 Module[{order = Last[FindShortestTour[p]]}, 
  If[RandomReal[] < .5, p[[Rest[order]]], p[[order]]]]
Graphics[line = Line /@ sortPoint /@ FindClusters[p, 5]]

Make it to be a graph

rule = Dispatch[MapIndexed[Rule[#, First[#2]] &, p]];
g = Graph[
  Catenate[Developer`PartitionMap[UndirectedEdge @@ # &, #, 2, 1] & /@
     Level[line /. rule, {2}]], 
  VertexCoordinates -> Reverse /@ Normal[rule]]

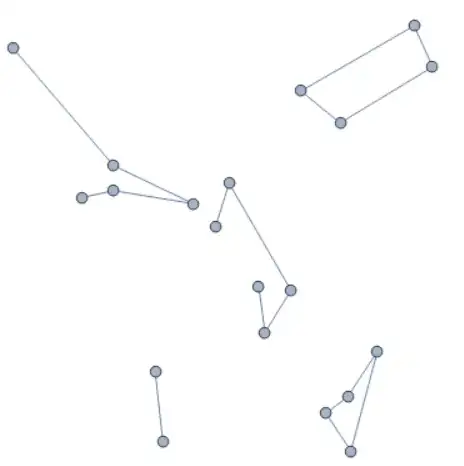
Add some additional edges between components each other

gLast = Fold[
  GraphUnion[#, #2, VertexCoordinates -> Reverse /@ Normal[rule], 
    VertexLabels -> "Name"] &, g, 
  Graph[UndirectedEdge @@@ Tuples[#]] & /@ 
   Subsets[ConnectedComponents[g], {2}]]

To make sure we can select these edge we want,we should make some essential variables.

var = Rule[addEdge @@ #, #] & /@ 
   Complement[EdgeList@gLast, EdgeList@g];
weightRule = 
  Rule[#, EuclideanDistance @@ (# /. Reverse /@ Normal[rule])] & /@ 
   Complement[EdgeList@gLast, EdgeList@g];
var2 = connectQ @@@ Keys[var];

But obviously the method of nikie's don't give integer always.

sol = Last[
   FindMinimum[{(Values[var] /. weightRule).var2, 
     And @@ Thread[0 <= var2 <= 1] && 
      And @@ Thread[
        Total /@ 
          Function[ind, Select[ind, MemberQ[var2, #] &]] /@ 
           Apply[connectQ, 
            IncidenceList[gLast, #] & /@ 
             ConnectedComponents[g], {2}] == 1]}, var2]];

As we see the result,we get some 0.5,neither 0 nor 1.But when we give a constraint such Element[var2, Integers].It will give some error information.

Values[sol] // Counts

<|1. -> 1, 0. -> 153, 0.5 -> 3|>

I think if we can solve this equation then the process in following become easy.Of course,if you have another smart solution,I'll glad to know.:)

ps: The result picture maybe like following.Of course,this is just an approximate guess.

score 5 · Accepted Answer · edited Jun 16 '20 at 09:23

The following code will help:

cc = ConnectedComponents@g;
pts = Map[{#, PropertyValue[{g, #}, VertexCoordinates]} &, cc, {2}];
pre = First@MinimalBy[#, Last] & /@ 
   Apply[{#1[[1]] <-> #2[[1]], Norm[#1[[2]] - #2[[2]]]} &, 
    Tuples /@ Subsets[pts, {2}], {2}];
spt = EdgeList@
   FindSpanningTree[
    CompleteGraph[Length@cc, EdgeWeight -> pre[[;; , 2]]]];
res = Extract[pre, 
   First@Position[
       UndirectedEdge @@@ Subsets[Range@Length@cc, {2}], #] & /@ spt];
res[[;; , 2]] // Total
HighlightGraph[g~EdgeAdd~res[[;; , 1]], res[[;; , 1]]]

Let me explain how this code works:

Our goal is to find a shortest connection between point groups (ConnectedComponents). So the first thing we should do is to find out the shortest distance between each tuple.

The first five lines of my code is doing this job: Find out ConnectedComponents, then determine those points' position. Finally create list pre by calculating the distance between each tuple of points in each tuple of ConnectedComponents and single out the shortest connection in each tuple of ConnectedComponents.
Find the shortest path that can connect this whole graph together.

If we want to get the shortest connection, then it must be a tree, FindSpanningTree will do the job~ Check the code generating spt.
Take the result and reform them into the form we would love to see.

Take the edges' in spt and reform them back to the edges in the original graph. Check the code generating res.
Presentation

Quite simple~ Check the rest of the code~

The result will be as follow:

the value shown in the graph is the minimum distance.

UPDATE

A version if you want to use it everywhere! The only thing you should do is paste this code everywhere and set the input graph's name to gorig!

l = VertexList@gorig;
coor = PropertyValue[{gorig, #}, VertexCoordinates] & /@ l;
g = Graph[Range@Length@l, EdgeList@gorig /. Thread[l -> Range@Length@l], 
   VertexCoordinates -> coor];
cc = ConnectedComponents@g;
pts = Map[{#, PropertyValue[{g, #}, VertexCoordinates]} &, cc, {2}];
pre = First@MinimalBy[#, Last] & /@ 
   Apply[{#1[[1]] <-> #2[[1]], Norm[#1[[2]] - #2[[2]]]} &, 
    Tuples /@ Subsets[pts, {2}], {2}];
spt = EdgeList@
   FindSpanningTree[
    CompleteGraph[Length@cc, EdgeWeight -> pre[[;; , 2]]]];
res = Extract[pre, 
   First@Position[
       UndirectedEdge @@@ Subsets[Range@Length@cc, {2}], #] & /@ spt];
res[[;; , 2]] // Total
HighlightGraph[g~EdgeAdd~res[[;; , 1]], res[[;; , 1]]]

NOOOOOOO!!! The exam has been cancelled cause someone comporomised the test material!!! — Wjx, Jun 10 '16 at 22:47
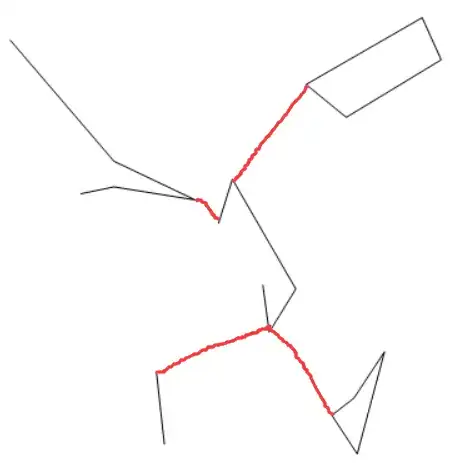
I have to say that your FindSpanningTree replace my FindMinimum is a wonderful idea. — yode, Jun 10 '16 at 23:41
Thanks very much.And I make a little change in this post last night.I hope you don't mind. :) And have you received the message I send you in chat room? — yode, Jun 11 '16 at 01:01
Nope......I didn't received any message still...... BTW, I don't mind at all~ see WTFPL~ BTW2: I think your question is all of high quality~ Really inspiring! — Wjx, Jun 11 '16 at 01:06

score 0 · Answer 2 · answered Feb 18 '17 at 08:22

Original method:

ConnectSeparateGraphCost[graph_] := 
 Module[{rule, cc, minWeightInCom, allMinEdge, spanTreeEdge, 
   completeGraph}, 
  rule = Dispatch[
    MapThread[Rule, {VertexList[graph], GraphEmbedding[graph]}]];
  cc = ConnectedComponents[graph];
  minWeightInCom = 
   First@MinimalBy[#, Last] & /@ 
    Map[{#, EuclideanDistance @@ (# /. rule)} &, 
     Tuples /@ Subsets[cc, {2}], {2}];
  allMinEdge = UndirectedEdge @@@ First /@ minWeightInCom;
  spanTreeEdge = 
   EdgeList[
    FindSpanningTree[
     completeGraph = 
      CompleteGraph[Length@cc, EdgeWeight -> Last /@ minWeightInCom]]];
  EdgeAdd[graph, 
   allMinEdge[[EdgeIndex[completeGraph, #] & /@ spanTreeEdge]]]]

Update the efficacy:

ConnectSeparateGraph[graph_] := 
 Module[{rule, pts, f, var1, var2, nearePoint, completeGraph}, 
  rule = Dispatch[
    MapThread[Rule, {VertexList[graph], GraphEmbedding[graph]}]];
  pts = WeaklyConnectedComponents[graph] /. rule;
  f = Nearest /@ Most[pts];
  var2 = Drop[pts, #] & /@ Range[Length[pts] - 1];
  var1 = MapThread[Catenate /@ # /@ #2 &, {f, var2}];
  nearePoint = 
   Catenate[
    Map[First[MinimalBy[#, EuclideanDistance @@ # &]] &, 
     Flatten[{var1, var2}, List /@ {2, 3, 4, 1, 5}], {2}]];
  completeGraph = 
   CompleteGraph[Length[pts], 
    EdgeWeight -> EuclideanDistance @@@ nearePoint];
  EdgeAdd[graph, 
   UndirectedEdge @@@ (nearePoint[[EdgeIndex[completeGraph, #] & /@ 
         EdgeList[FindSpanningTree[completeGraph]]]] /. 
      Reverse /@ Normal[rule])]]

When the separate component is 50:

g=(Uncompress@*FromCharacterCode@*Flatten@*(ImageData[#1, "Byte"] &)@*
   Import)["https://ooo.0o0.ooo/2017/02/18/58a8035aae255.png"];

ConnectSeparateGraphCost[g]; // AbsoluteTiming(*old method*)
ConnectSeparateGraph[g]; // AbsoluteTiming(*updated method*)
ConnectSeparateGraphCost[g] == ConnectSeparateGraph[g]

{2.18698, Null}

{0.329665, Null}

True

How to connect some separate components with shortest total length line

2 Answers2

UPDATE

Linked