How to rapidly find the nearest pairs of points in different clusters

Question

Background

For speed up this question or this question,I have such need.

Current try:

Suppose I have $3$ clusters of points:

list = {{{0, 0}, {.2, 0}}, {{2, 1}, {2, 2}, {2, 2.5}}, {{1.5, 
     6}, {1.6, 7}, {1.4, 8}, {1.9, 10}}};
plot = ListPlot[list, Axes -> False, Frame -> True, PlotLegends ->Automatic,
  FrameTicks -> None]

I want to find the closest pairs of points, each point in a different cluster. My current method:

Method one based on Tuples

tuplesMethod[list_] := 
 First[MinimalBy[Tuples[#], EuclideanDistance @@ # &]] & /@ 
  Subsets[list, {2}]

Method two based on Nearest

nearestMethod[list_] := 
 Module[{f, var1, var2}, f = Nearest /@ Most[list];
  var2 = Drop[list, #] & /@ Range[Length[list] - 1];
  var1 = MapThread[Catenate /@ # /@ #2 &, {f, var2}];
  Catenate[
   Map[First[MinimalBy[#, EuclideanDistance @@ # &]] &, 
    Flatten[{var1, var2}, List /@ {2, 3, 4, 1, 5}], {2}]]]

Usage:

minDistPoints = tuplesMethod[list]

{{{0.2,0},{2,1}},{{0.2,0},{1.5,6}},{{2,2.5},{1.5,6}}}

Show it:

Show[plot, Epilog -> Line /@ minDistPoints]

Question

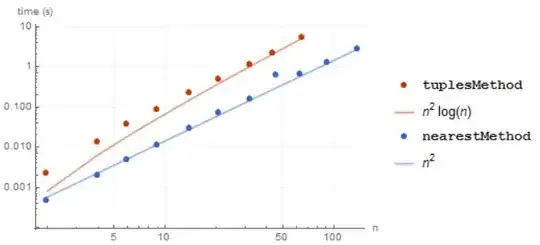
But the current method is too slow, if clusters up to 10,the execution time will be cannot stand:

testPoint[n_] := (SeedRandom[2];
  FindClusters[RandomReal[10 n, {20 n, 2}], n])

GeneralUtilities`BenchmarkPlot[{tuplesMethod, 
  nearestMethod}, testPoint, 2, TimeConstraint -> 50, 
 "IncludeFits" -> True]

Answer 1

The Nearest method should do well, but you need to make sure that it is only applied once for each cluster. Here is how I would code it. First a helper function, that finds the nearest members between one cluster and a list of other clusters:

icluster[i_, rest_]:=Module[{r, near,distances, rank,pos},
    (* create a single list of other points *)
    r = Catenate[rest];

    (* apply NearestFunction to the list of other points *)
    near = Nearest[i][r][[All, 1]];

    (* compute distance squared between the nearest member and the other point *)
    distances = Total[(near-r)^2, {2}];

    (* rank the distances *)
    rank = Ordering @ Ordering @ distances;

    (* find the minimum rank for each cluster. Probably could be sped up *)
    pos = Flatten @ Position[
        rank,
        Alternatives @@ Min /@ Internal`PartitionRagged[rank, Length/@rest]
    ];

    (* extract near point and other points for minimum ranks *)
    Transpose[{near[[pos]], r[[pos]]}]
]

We use this helper function to get the members of the clusters closest to each other:

nearestClusterMembers[list_] := Catenate @ Table[
    icluster[list[[i]], list[[i+1 ;; -1]]],
    {i, Length[list]-1}
]

For your simple example:

nearestClusterMembers[
    {
    {{0,0},{.2,0}},
    {{2,1},{2,2},{2,2.5}},
    {{1.5,6},{1.6,7},{1.4,8},{1.9,10}}
    }
]

{{{0.2, 0}, {2, 1}}, {{0.2, 0}, {1.5, 6}}, {{2, 2.5}, {1.5, 6}}}