FindCurvePath for lines (rather than points)

Question

I have need of a function to find a good ordering for a series of lines, as FindCurvePath does for points.

Sample data:

dat = {{{-2.83718,1.},{-2.83708,0.999885}},{{-2.837,0.999875},
{-2.83708,0.999885}},{{-2.83649,0.999763},{-2.83673,0.999716}},
{{-2.83673,0.999716},{-2.837,0.999875}},{{-2.83747,0.999718},{-2.83718,1.}},
{{-2.83699,0.999714},{-2.83697,0.999704}},{{-2.83696,0.999716},
{-2.8368,0.999686}},{{-2.83696,0.999716},{-2.83697,0.999704}},
{{-2.83678,0.999668},{-2.8368,0.999686}},{{-2.83702,0.999653},
{-2.83699,0.999714}},{{-2.83675,0.999644},{-2.83678,0.999668}},
{{-2.83647,0.999632},{-2.83649,0.999763}},{{-2.83647,0.999632},
{-2.8365,0.999633}},{{-2.8367,0.999603},{-2.83675,0.999644}},
{{-2.8365,0.999633},{-2.83654,0.999584}},{{-2.83666,0.99957},
{-2.8367,0.999603}},{{-2.83728,0.999697},{-2.83712,0.999592}},
{{-2.83664,0.999553},{-2.83666,0.99957}},{{-2.83654,0.999584},
{-2.83655,0.999551}},{{-2.83655,0.999551},{-2.83656,0.999549}},
{{-2.83712,0.999592},{-2.83702,0.999653}},{{-2.83656,0.999549},
{-2.83664,0.999553}}};

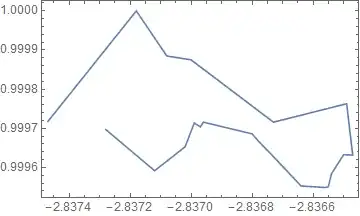
These lines form a single line:

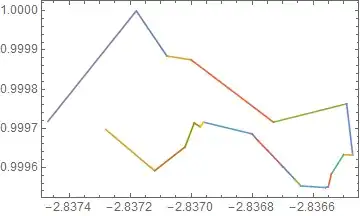
ListLinePlot[dat, Frame -> True]

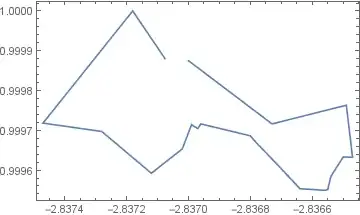
But they are out of order and their directions are mixed:

ListLinePlot[Join @@ dat, Frame -> True]
Graphics[Arrow @ dat, Frame -> True]

So I need not only to order the lines but to reverse some of them as well.

I also need to allow for gaps between lines. End points will not always be as close as in this example. A solution should work also on:

dat2 = dat ~Delete~ {{2}, {8}, {9}, {13}};

ListLinePlot[dat2, Frame -> True]

Additionally in practice my constituent lines are more than two points long but the end points should be sufficient for a solution. However I either need ordering and direction data that I can apply to the full lines or an algorithm that works on compound lines, not just line segments.

---

Benchmarking

With multiple methods posted it is time to being benchmarking. The three methods are not entirely equivalent but I am making an effort to compare them as fairly as I can.

• Feyre's code does not return an explicit order but instead modified data
• my code is dependent on the specification of a suitable search radius
• Simon's FindShortestTour does not return an order starting with one of the ends
• I had to make a change and an addition to Simon's code to get consistent results
• I do not include application of the ordering produced by segOrder1 and segOrder2 in the benchmark but I found the overhead for that operation negligible

For random data I am using:

rdat[n_] := 
  RandomSample /@ Partition[RandomReal[1, {n, 2}], 2, 1] // RandomSample

The functions as I am benchmarking them:

segOrder1[segs_, rad_: 0.0001] := (
   Flatten[segs, 1]
     // Nearest[# -> Automatic, #, {2, rad}] &
     // Cases[{_, _}]
     // Join[#, Partition[Range[2 Length@segs], 2]] &
     // Graph
     // FindPath[#, ## & @@ GraphPeriphery[#]] &
     // First
  )

segOrder2[segs_] :=
  Module[{d = Flatten[segs, 1], dist},
    dist[a_?OddQ, b_] /; (b == a + 1) := 0;
    dist[a_, b_] := 1 + EuclideanDistance[d[[a]], d[[b]]];

    FindShortestTour[Range @ Length @ d, DistanceFunction -> dist][[2]]
      // If[#[[2]] === 2, Most, Rest][#] &
  ]

segReorder[dat_] :=
 Module[{newdat, z, k, temp, it},
  newdat = {dat[[1]]};
  z = 1; k = 1;
  While[k < Length@dat, 
   temp = Select[dat, FreeQ[Join[Reverse /@ newdat, newdat], #] &];
   it = Table[
     RegionDistance[Line@newdat[[k]], temp[[i, j]]], {i, Length[dat] - k}, {j, 2}];
   z = Position[it, Min@it][[1, 1]];
   If[it[[z, 1]] > it[[z, 2]], AppendTo[newdat, Reverse@temp[[z]]], 
    AppendTo[newdat, temp[[z]]]]; k++;];
  newdat
  ]

Confirmation that they are working on this data:

SeedRandom[1]
dat = rdat[20];
o1 = segOrder1[dat];
o2 = segOrder2[dat];
newdat = segReorder[dat];

Partition[Flatten[dat, 1][[#]], 2] & /@ {o1, o2};
Append[%, newdat];
Graphics[Arrow@#, ImageSize -> 200] & /@ % // Row

Benchmark Plot

Needs["GeneralUtilities`"]

BenchmarkPlot[{segOrder1, segOrder2, segReorder}, rdat, 5]

Answer 1

Using FindShortestTour with a custom distance function:

d = Flatten[dat, 1];

dist[a_?OddQ, b_] /; (b == a + 1) := 0.0001 EuclideanDistance[d[[a]], d[[b]]]

dist[a_, b_] := EuclideanDistance[d[[a]], d[[b]]]

o = Most@FindShortestTour[Range[Length@d], DistanceFunction -> dist][[2]]
(* {1, 2, 4, 3, 8, 7, 6, 5, 24, 23, 25, 26, 29, 30, 37, 38, 39, \
40, 43, 44, 35, 36, 31, 32, 27, 28, 21, 22, 17, 18, 14, 13, 15, 16, \
12, 11, 20, 19, 42, 41, 34, 33, 9, 10} *)

Graphics[Arrow /@ Partition[d[[o]], 2]]

Update

A revised version which addresses Mr.Wizard's observations. Performance is still poor though.

segOrder2[segs_] :=
 Module[{d = Flatten[segs, 1], dist, o},
  dist[a_?OddQ, b_] /; (b == a + 1) := 0;
  dist[a_, b_] := 1 + EuclideanDistance[d[[a]], d[[b]]];
  o = FindShortestTour[Range[Length@d], DistanceFunction -> dist][[2]] // 
    If[#[[2]] === 2, Rest, Most][#] &;
  RotateLeft[o, 2 Ordering[dist @@@ Partition[o, 2], -1] - 1]]

Answer 2

This approach generates the data into newdat.

newdat = {dat[[1]]};
z = 1; k = 1;
While[k < Length@dat, 
 temp = Select[dat, FreeQ[Join[Reverse /@ newdat, newdat], #] &];
 it = Table[
   RegionDistance[Line@newdat[[k]], temp[[i, j]]], {i, 
    Length[dat] - k}, {j, 2}];
 z = Position[it, Min@it][[1, 1]];
 If[it[[z, 1]] > it[[z, 2]], AppendTo[newdat, Reverse@temp[[z]]], 
  AppendTo[newdat, temp[[z]]]]; k++;]

And the results:

ListLinePlot[Join @@ newdat, Frame -> True]
Graphics[Arrow@newdat, Frame -> True]

For the reduced data one arrow stays reversed.

Answer 3

With the missing piece from How do I "read out" the vertex names on this graph? I can self-answer using Nearest and Graph. Please don't let this post discourage answering as I am eager to see other approaches.

Now as a function with at least a little reusability. The second parameter is the search radius.

segOrder[segs_, rad_: 0.0001] := (
   Flatten[segs, 1]
     // Nearest[# -> Automatic, #, {2, rad}] &
     // Cases[{_, _}]
     // Join[#, Partition[Range[2 Length@segs], 2]] &
     // Graph
     // FindPath[#, ## & @@ GraphPeriphery[#]] &
     // First
  )

ListLinePlot[Part[Join @@ dat, segOrder[dat]], Frame -> True]

It works on the set with gaps given a sufficient radius:

ListLinePlot[Part[Join @@ dat2, segOrder[dat2, 0.0001]], Frame -> True]

Extension

Here is my application of this ordering to the sorting (and joining) of longer lines.

lineSort[lines_, r_: 0.0001] :=
  lines[[All, {1, -1}]] ~segOrder~ r ~Partition~ 2 //
    Cases[ {a_, b_} :> lines[[⌈a/2⌉, b - a ;; a - b ;; b - a]] ]

Now I can do things like this:

geo = Import["http://www.rr4w.com/kml/9.kml"];

Cases[geo, Line[x_] :> x, {-4}] // lineSort // Catenate;

Graphics[{
  Thickness[1/150], 
  Line[%, VertexColors -> Array[ColorData["Rainbow"], Length@%, {0, 1}]]
}]

Answer 4

For the sake of general,such as the line include not only $2$ points,the every line maybe is a mess order(include first one),I make some adjust like following.Maybe too long,but powerful.

If you have a gap data like dat2

We can convert it into non-gap data first by ConnectComponentPoints

ConnectComponentPoints[p_] := 
 Module[{f, var1, var2, nearePoint, graph}, f = Nearest /@ Most[p];
  var2 = Drop[p, #] & /@ Range[Length[p] - 1];
  var1 = MapThread[Catenate /@ # /@ #2 &, {f, var2}];
  nearePoint = 
   Catenate[
    Map[First[MinimalBy[#, EuclideanDistance @@ # &]] &, 
     Flatten[{var1, var2}, List /@ {2, 3, 4, 1, 5}], {2}]];
  graph = 
   CompleteGraph[Length[p], 
    EdgeWeight -> EuclideanDistance @@@ nearePoint];
  Join[p, 
   nearePoint[[EdgeIndex[graph, #] & /@ 
      EdgeList[FindSpanningTree[graph]]]]]]
ListLinePlot[ConnectComponentPoints[dat2]]

http://o8aucf9ny.bkt.clouddn.com/2017-02-18-20-30-50.png

If you have a non-gap data like dat:

ConnectLines[dat_] := 
 Module[{g = 
    SimpleGraph[RelationGraph[IntersectingQ, dat], 
     VertexLabels -> "Index"], path}, 
  path = FindShortestPath[g, Sequence @@ GraphPeriphery[g]];
  Append[First /@ #, #[[-1, -1]]] &[
   FoldPairList[(Transpose[
        DeleteDuplicates[
         SortBy[Tuples[{##}], N[EuclideanDistance @@ #] &], 
         ContainsAny]] // {Reverse[#], #2} & @@ # &) &, First[path], 
    Rest[path], Identity]]]
newdat = ConnectLines[dat];
ListLinePlot[Join @@ newdat, Frame -> True]
Graphics[Arrow@newdat, Frame -> True]

http://o8aucf9ny.bkt.clouddn.com/2017-02-18-20-28-53.png