1

I wanted to simplify this nasty equation, which I couldn't seem to format also properly.

$U[k_]:= 1/2 E^(-I k) (2 E^(I k)
 Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] - Sqrt[
   4 E^(2 I k)
  Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[F]^2 - 
2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])])
PowerExpand@FullSimplify[$U];(* This won't simplify anything, eventhough simplification exist just by seeing *)

Are there any other command which simplify this expression? I need to later do plotting.

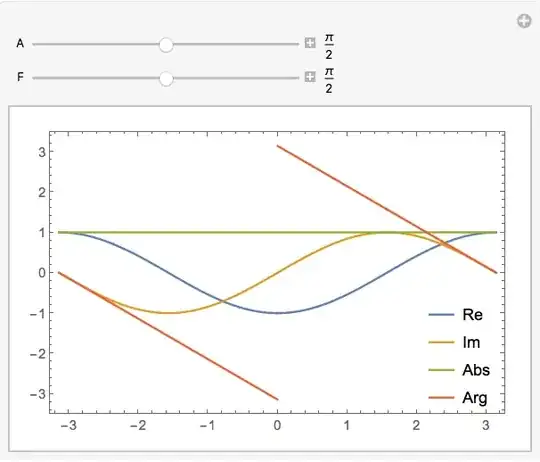
    Manipulate[Plot[$U[k], {k, -\[Pi], \[Pi]}, 
  PlotLegends -> "Expressions"], {A, 
  0, \[Pi]}, {F, 0, \[Pi]}]

This is what I getting: enter image description here

I strongly apologies for the formatting of my text, but I don't know how to put it properly.

Shamina
  • 633
  • 4
  • 16
  • [$U] should be [$U[k]]. There are no obvious simplifications. From documentation for PowerExpand "PowerExpand in general disregards all issues of branches of multivalued functions, so may not preserve the numerical values of expressions." Consequently, use only when you know that operation is safe. In general, add Assumptions (constraints) or use Assuming to assist simplification. – Bob Hanlon Apr 10 '17 at 17:59

1 Answers1

5

Since $U[k] is complex, in addition to assigning numeric values to A and F you must use Re, Im, Abs, or Arg to Plot.

Due to scoping issues with Manipulate, you need to define $U with three arguments or move the definition of $U into the Manipulate.

$U[k_, A_, F_] := 
  1/2 E^(-I k) (2 E^(I k) Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] - 
     Sqrt[4 E^(2 I k) Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[
          F]^2 - 2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])]);

Manipulate[
 Plot[Evaluate[#@$U[k, A, F] & /@ {Re, Im, Abs, Arg}], {k, -Pi, Pi},
  Frame -> True, Axes -> False, 
  PlotLegends -> Placed[{"Re", "Im", "Abs", "Arg"}, {0.9, 0.2}]],
 {{A, Pi/2}, 0, Pi, Appearance -> "Labeled"},
 {{F, Pi/2}, 0, Pi, Appearance -> "Labeled"}]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Thanks a lot for this. But I am not able to reproduce it on my Mathematica 11.1. This is what I am getting. So, no plot unfortunately. – Shamina Apr 11 '17 at 07:25
  • 1
    @Shamina - the error message clearly shows that an old definition for $U is precluding the new definition from working. Start with a fresh kernel and reevaluate the code. – Bob Hanlon Apr 11 '17 at 13:58
  • I was facing some problem, so thought of clearing them. If I have say two functions(or multiple) $U1 and $U2. How to implement it? I got stuck and getting some weird plots. e.g. $U2 = -$U1 – Shamina Apr 19 '17 at 12:03
  • @Shamina - Post a question (including your data and code for a minimal working example) and explain what you are trying to do and what you expect as output. – Bob Hanlon Apr 19 '17 at 14:57
  • Should I post a new question or editing this one will work? – Shamina Apr 19 '17 at 15:09
  • @Shamina - Post a new question. – Bob Hanlon Apr 19 '17 at 15:12
  • Here it is, I hope it is clear. https://mathematica.stackexchange.com/questions/143971/plotting-complex-functions-using-manipulate – Shamina Apr 19 '17 at 15:24