Plot and an error

Question

I have set of matrices(multiplied to give U123[q, p, r]) and would like to diagonalize U123[q, p, r] and plot the eigenvalues. Fortunately, after some try I was able to get out of the Root. For this, I used dynamic calculation (dynamically giving values to the variables and calculating the eigenvalues inside the Module).

Element[k, Reals];
H31[q_] := {{0, 0, q Exp[I k]}, {0, 0, 0}, {q  Exp[-I k], 0, 0}};
H12[p_] := {{0, p, 0}, {p, 0, 0}, {0, 0, 0}};
H23[r_] := {{0, 0, 0}, {0, 0, r}, {0, r, 0}};

(*FullSimplify[PowerExpand@MatrixExp[-I  H31].MatrixExp[-I  H12].\
MatrixExp[-I  H23].MatrixExp[-I  H12]];*)

U123[q_, p_, r_] := 
  MatrixExp[-I  H31[q]].MatrixExp[-I  H23[r]].MatrixExp[-I  H12[p]];

quit[q_, p_, r_] := 
 Module[{$ph}, $ph = -I Log[Eigenvalues[U123[q, p, r]]];
  Plot[Evaluate@Flatten[Through[{Re}[$ph]]], {k, -Pi, Pi}, 
   Frame -> True, 
   PlotLegends -> {"Re $ph1", "Re $ph2", "Re $ph3"}]]
Manipulate[
 quit[q, p, r], {{q, Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{p, 3 Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{r, Pi/4}, 0, 2 Pi, 
  Appearance -> "Labeled"}]

The problem I am facing now is, I can freely change p and r but not q (which supposed to work like them p and r).

This what I getting after changing q, even by a very small value. Only thing I am able to do is that I am able to change the values for q here {{q, Pi/2}, 0, 2 Pi, Appearance -> "Labeled"}. Then it works but not through sliding.

Can this graph be resolved, as I am getting this also:

I have no idea how to solve this. To get even this much working, I am very thankful to the solutions I received at this and this from @Bob Hanlon and @yohbs.

related https://mathematica.stackexchange.com/q/111315/2079 and https://mathematica.stackexchange.com/q/51776/2079 — george2079, May 02 '17 at 19:20
also related: https://mathematica.stackexchange.com/questions/39747/how-to-plot-several-functions-without-jumping-multiple-eigenvalues-of-a-system — egwene sedai, May 02 '17 at 19:32
Thanks @george2079. I got the answer(originally posted by you). But can it be simplified, it seems to be going over the head or it is not possible? Any of your thoughts will be valuable. There is also some problem of Re, Im part for the plot of $ph = -I Log[Eigenvalues[U123[q, p, r]]]. — Shamina, May 03 '17 at 09:15

egwene sedai · Answer 1 · 2017-05-03T13:49:05.540

Adapted from the code in Reordering numerically calculated eigenvalues assuming smooth dependence on a parameter

Clear["Global`*"]
Element[k, Reals];
H31[k_, q_] := {{0, 0, q (Cos[k] + I Sin[k])}, {0, 0, 
    0}, {q (Cos[k] + I Sin[k]), 0, 0}};
H12[p_] := {{0, p, 0}, {p, 0, 0}, {0, 0, 0}};
H23[r_] := {{0, 0, 0}, {0, 0, r}, {0, r, 0}};

(*FullSimplify[PowerExpand@MatrixExp[-I H31].MatrixExp[-I \
H12].MatrixExp[-I H23].MatrixExp[-I H12]];*)

U123[k_?NumericQ, q_?NumericQ, p_?NumericQ, r_?NumericQ] := 
  MatrixExp[-I H31[k, q]].MatrixExp[-I H23[r]].MatrixExp[-I H12[
       p]] // N;

q = \[Pi]/2;
p = 3 \[Pi]/2;
r = \[Pi]/4;
c = {};
frames = {};
xvals = Pi Range[-1, 1, 1/100];
alle = Table[({k, #} & /@ (-I Log[Eigenvalues[U123[k, q, p, r]]] // 
   Re)), {k, xvals}];
colors = {RGBColor[0.368417, 0.506779, 0.709798], RGBColor[
   0.880722, 0.611041, 0.142051], RGBColor[
   0.560181, 0.691569, 0.194885]};
Clear[g];
Monitor[Do[
  line = First@Position[alle, First@SortBy[#, #[[2]] &]] & /@ 
    alle[[;; 2]];
  MapIndexed[(nextx = #;
     proj = {nextx, 
       Quiet[Interpolation[alle[[Sequence @@ #]] & /@ line]@nextx]};
     AppendTo[line, 
      Position[alle, 
        First@Nearest[alle[[First@#2 + 2]], proj]][[1]]]) &, 
   xvals[[3 ;;]]];
  AppendTo[c, alle[[Sequence @@ #]] & /@ line];
  alle = Delete[alle, line];
  AppendTo[frames, 
   g = Show[{If[Length@First@alle > 0, ListPlot[Flatten[alle, 1]], 
       Graphics[]], 
      Graphics[
       MapIndexed[{Thick, colors[[First@#2]], Line[#]} &, c]]}, 
     PlotRange -> All, AxesOrigin -> {0, 0}]], {nrem, 3, 1, -1}], g]
Graphics[MapIndexed[{Thick, colors[[First@#2]], Line[#]} &, c], 
 Axes -> True]

before:

after:

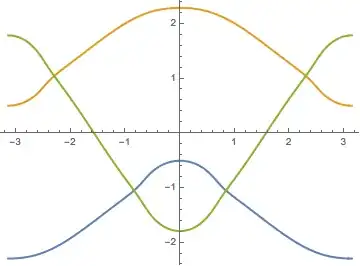
edit:

to put the above inside Manipulate, just wrap it inside a function e.g. plotevs[...] that returns the figure, like this:

Element[k, Reals];
H31[k_, q_] := {{0, 0, q (Cos[k] + I Sin[k])}, {0, 0, 
    0}, {q (Cos[k] + I Sin[k]), 0, 0}};
H12[p_] := {{0, p, 0}, {p, 0, 0}, {0, 0, 0}};
H23[r_] := {{0, 0, 0}, {0, 0, r}, {0, r, 0}};

(*FullSimplify[PowerExpand@MatrixExp[-I H31].MatrixExp[-I \
H12].MatrixExp[-I H23].MatrixExp[-I H12]];*)

U123[k_?NumericQ, q_?NumericQ, p_?NumericQ, r_?NumericQ] := 
  MatrixExp[-I H31[k, q]].MatrixExp[-I H23[r]].MatrixExp[-I H12[
       p]] // N;

plotevs[q_, p_, r_] := Module[{},
  c = {};
  frames = {};
  xvals = Pi Range[-1, 1, 1/100];
  (*alle=Table[{{xvals[[k]],xvals[[k]],xvals[[k]]},-I Log[Eigenvalues[
  U123[xvals[[k]],q,p,r]]]//Re}\[Transpose],{k,1,Length[xvals]}];*)

  alle = Table[({k, #} & /@ (-I Log[Eigenvalues[U123[k, q, p, r]]] // 
        Re)), {k, xvals}];
  colors = {RGBColor[0.368417, 0.506779, 0.709798], RGBColor[
    0.880722, 0.611041, 0.142051], RGBColor[
    0.560181, 0.691569, 0.194885]};
  Clear[g];
  Do[line = 
    First@Position[alle, First@SortBy[#, #[[2]] &]] & /@ 
     alle[[;; 2]];
   MapIndexed[(nextx = #;
      proj = {nextx, 
        Quiet[Interpolation[alle[[Sequence @@ #]] & /@ line]@nextx]};
      AppendTo[line, 
       Position[alle, First@Nearest[alle[[First@#2 + 2]], proj]][[
        1]]]) &, xvals[[3 ;;]]];
   AppendTo[c, alle[[Sequence @@ #]] & /@ line];
   alle = Delete[alle, line];
   (*AppendTo[frames,g=Show[{If[Length@First@alle>0,ListPlot[Flatten[
   alle,1]],Graphics[]],Graphics[MapIndexed[{Thick,colors[[First@#2]],
   Line[#]}&,c]]},PlotRange\[Rule]All,AxesOrigin\[Rule]{0,
   0}]]*), {nrem, 3, 1, -1}];
  Return[Graphics[
    MapIndexed[{Thick, colors[[First@#2]], Line[#]} &, c], 
    Axes -> True]]
  ]

then use Manipulate[] as before:

Manipulate[
 plotevs[q, p, r], {{q, Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{p, 3 Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{r, Pi/4}, 0, 2 Pi, 
  Appearance -> "Labeled"}]

Thanks for this. But it seems very complicated to understand. Is this is Real part plot or something else? As it is not matching with my plot for same values of q, p and r. Now I am suspicious about my result. — Shamina, May 03 '17 at 09:42
@Shamina the figures I posted as example matched the answer you posted with the q,p,r taken to be the initial value in Manipulate[]: q = \[Pi]/2, p = 3 \[Pi]/2, r = \[Pi]/4. and is only the real part of -I Log[Eigenvalues[U123[k, q, p, r]]]. It is plotted by making a table alle={{{kvalue1,eigen1},{kvalue1,eigen2},{kvalue1,eigen2}},{{kvalue2,eigen1},{kvalue2,eigen2},{kvalue2,eigen2}}...} — egwene sedai, May 03 '17 at 12:57
Plots are not same. I checked. If we take p -> 4.80035,r -> 1.58336, q -> 4.86319}. It behaves very badly — Shamina, May 03 '17 at 13:50
@Shamina the answer from the reference link assumes smooth dependence on a parameter. in some cases it may indeed fail, like the example p -> 4.80035,r -> 1.58336, q -> 4.86319. I do not yet now how to get around that. If you do not care about assigning different colors to different eigenvalues, you can always delete everything under alle=Table[...] and just use ListPlot[alle, PlotStyle -> Blue] — egwene sedai, May 03 '17 at 14:39
@Shamina additionally, for that particular example (p -> 4.80035,r -> 1.58336, q -> 4.86319), use more sample points with xvals = Pi Range[-1, 1, 1/500]; seems to work. code may need to run for a couple of minutes. — egwene sedai, May 03 '17 at 14:43
Just last disturbance, alle = Table[({k, #} & /@ (-I Log[Eigenvalues[U123[k, q, p, r]]] // Re)), {k, xvals}]; Here even Re[-I Log[Eigenvalues[U123[k, q, p, r]]]] will work? — Shamina, May 03 '17 at 15:38
@Shamina I think so: https://reference.wolfram.com/language/ref/Postfix.html — egwene sedai, May 03 '17 at 15:47

score 2 · Accepted Answer · answered May 02 '17 at 18:11

Thanks to you all again.
I was able to get answer partly (still great help, after working on the problem). I was able to resolve the first problem of the that blue color error plot but not second one.
Here is the answer:

Element[k, Reals];
H31[q_] := {{0, 0, q  (Cos[k] + I Sin[k])}, {0, 0, 0}, {q  (Cos[k] + I Sin[k]), 0, 0}};
H12[p_] := {{0, p, 0}, {p, 0, 0}, {0, 0, 0}};
H23[r_] := {{0, 0, 0}, {0, 0, r}, {0, r, 0}};

(*FullSimplify[PowerExpand@MatrixExp[-I  H31].MatrixExp[-I  H12].\
MatrixExp[-I  H23].MatrixExp[-I  H12]];*)

U123[q_, p_, r_] := 
  MatrixExp[-I  H31[q]].MatrixExp[-I  H23[r]].MatrixExp[-I  H12[p]];

quit[q_, p_, r_] := 
 Module[{$ph}, $ph = -I Log[Eigenvalues[U123[q, p, r]]];
  Plot[Evaluate@Flatten[Through[{Re}[$ph]]], {k, -Pi, Pi}, 
   Frame -> True, 
   PlotLegends -> {"Re $ph1", "Re $ph2", "Re $ph3"}]]
Manipulate[
 quit[q, p, r], {{q, Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{p, 3 Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{r, Pi/4}, 0, 2 Pi, 
  Appearance -> "Labeled"}]

I just redefined Exp[I k] = (Cos[k] + I Sin[k]). However, I don't have a single idea of the fact that why it worked, also of the second problem.

Plot and an error

2 Answers2

Linked