0

This is in continuation with How to simplify this?. But I will try to make it self contained.

I need to do a plotting of two complex valued functions, without removing any branches or anything like that.

After I got a very nice answer for the above mentioned previous question(for one function), this is for two function:

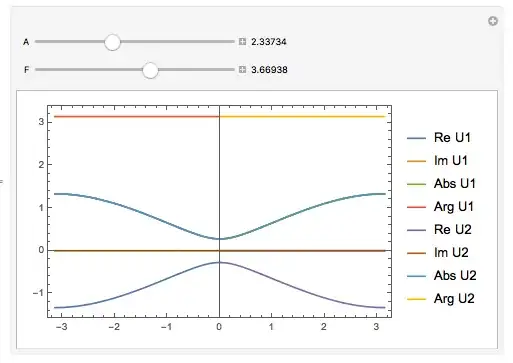
$U1[k_,A_,F_]:= 1/2 E^(-I k) (2 E^(I k)
 Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] - Sqrt[
  4 E^(2 I k) Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[F]^2 - 
  2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])]);

 $U2[k_,A_,F_]:= 1/2 E^(-I k) (2 E^(I k)
 Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] + Sqrt[4 E^(2 I k)
  Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[F]^2 - 
  2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])])

 $logU1[k_,A_,F_] = -I Log[$U1[k,A,F]];

 $logU2[k_,A_,F_] = -I Log[$U2[k,A,F]];

 Manipulate[Plot[{Evaluate[#@ $logU1[k,A,F] & /@ {Re, Im, Abs, Arg}], Evaluate[#@ $logU2[k,A,F] & /@ {Re, Im, Abs, Arg}]}, {k, -Pi, Pi}, Frame -> True, Axes -> False, PlotLegends -> Placed[{"Re", "Im", "Abs", "Arg"}, {0.9, 0.2}]], {{A, Pi/2}, 0, 2 Pi, Appearance -> "Labeled"}, {{F, Pi/2}, 0, 2 Pi, Appearance -> "Labeled"}]

This is not giving the desired result. Which is two merged solutions in a single graph.

In summary: generalizing to many input functions.

Shamina
  • 633
  • 4
  • 16
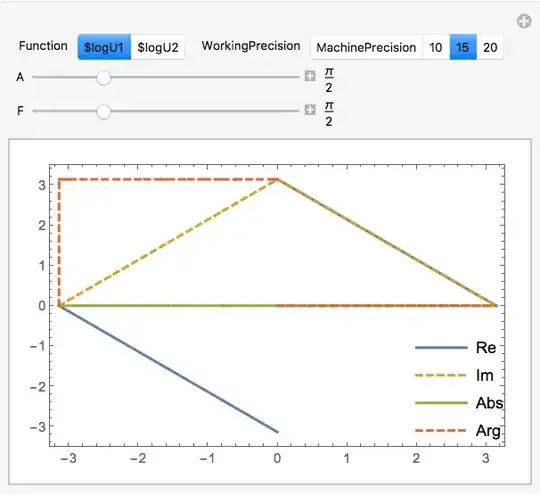
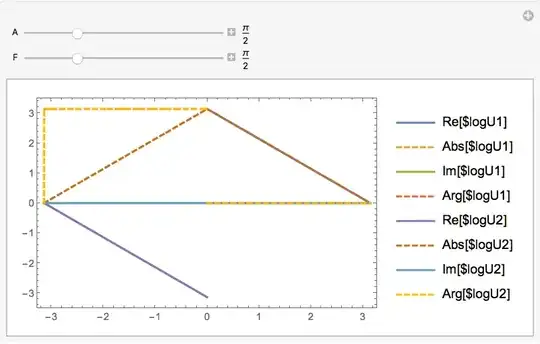
  • You have a typo. You define twice $logU1 and the second one should probably be $logU2 – yohbs Apr 19 '17 at 15:27
  • Thanks @yohbs, I corrected it(it was only here). – Shamina Apr 19 '17 at 15:28
  • Also, consider using Through which is nicer than the Evaluate[#@ ...] construct: Through[{Re, Im, Abs, Arg}[$logU1[k, A, F]]] – yohbs Apr 19 '17 at 15:30
  • Lastly, I don't understand what the problem is. What do you want to plot? – yohbs Apr 19 '17 at 15:30
  • Thanks for your points @yohbs. I would like to plot $logU1[k, A, F] and $logU2[k, A, F], in same plot with A, F slider. I hope it is clear – Shamina Apr 19 '17 at 15:32

2 Answers2

2

First, it's nicer to add a tiny imaginary offset so that the argument will not jump randomly from $-\pi$ to $\pi$:

$logU1[k_, A_, F_] = -I Log[$U1[k, A, F]] + 10^-6 I;
$logU2[k_, A_, F_] = -I Log[$U2[k, A, F]] + 10^-6 I;

Second, I think this is what you're trying to do:

Manipulate[Plot[Evaluate@Flatten[{
     Through[{Re, Im, Abs, Arg}[$logU1[k, A, F]]],
     Through[{Re, Im, Abs, Arg}[$logU2[k, A, F]]]
     }]
  , {k, -Pi, Pi}, Frame -> True,
  PlotLegends -> {"Re U1", "Im U1", "Abs U1", "Arg U1", "Re U2", 
    "Im U2", "Abs U2", "Arg U2"}], {{A, Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}, {{F, Pi/2}, 0, 2 Pi, 
  Appearance -> "Labeled"}]

enter image description here

yohbs
  • 7,046
  • 3
  • 29
  • 60
  • Thanks. Yes this what I was looking for. This offset is need to be removed later? Is this Through like Apply. Sorry for so many ques. – Shamina Apr 19 '17 at 16:04
1
$U1[k_, A_, F_] := 
  1/2 E^(-I k) (2 E^(I k) Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] - 
     Sqrt[4 E^(2 I k) Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[
          F]^2 - 2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])]);

$U2[k_, A_, F_] := 
 1/2 E^(-I k) (2 E^(I k) Cos[A] Cos[F] - (1 + E^(2 I k)) Sin[A] Sin[F] - 
    Sqrt[4 E^(2 I k) Cos[A]^2 Cos[F]^2 + (1 + E^(2 I k))^2 Sin[A]^2 Sin[
         F]^2 - 2 E^(2 I k) (2 + Cos[k] Sin[2 A] Sin[2 F])])

$logU1[k_, A_, F_] = -I Log[$U1[k, A, F]];

$logU2[k_, A_, F_] = -I Log[$U2[k, A, F]];

When having problems with a complicated problem look at its parts. Note that the Arg does not evaluate well with WorkingPrecision and requires arbitrary precision. This in turn requires that the Manipulate controls' output have sufficient precision to support arbitrary precision.

Sequencing of functions was changed to make it somewhat easier to tell when overlap occurs. Precision of A and F increased to support arbitrary precision.

Manipulate[
 Module[{
   A = SetPrecision[a, 2 prec],
   F = SetPrecision[f, 2 prec]},
  Plot[Evaluate[
    #@func[k, A, F] & /@
     {Re, Abs, Im, Arg}], {k, -Pi, Pi},
   WorkingPrecision -> prec,
   PlotStyle -> {Thick, Directive[Thick, Dashed]},
   PlotPoints -> 50,
   PlotRange -> {Automatic, {-3.5, 3.5}},
   Frame -> True,
   Axes -> False,
   PlotLegends -> Placed[
     {"Re", "Im", "Abs", "Arg"}, {0.9, 0.2}]]],
 Row[{
   Control[{{func, $logU1, "Function"}, {$logU1, $logU2}}],
   Spacer[10],
   Control[{{prec, 15, "WorkingPrecision"},
     {MachinePrecision, 10, 15, 20}}]}],
 {{a, Pi/2, "A"}, 0, 2 Pi,
  Appearance -> "Labeled"},
 {{f, Pi/2, "F"}, 0, 2 Pi, Appearance -> "Labeled"}]

enter image description here

For the combined Plot, you need to use a single Evaluate around the entire first argument to Plot.

Manipulate[
 Module[{
   A = SetPrecision[a, 40],
   F = SetPrecision[f, 40]},
  Plot[
   Evaluate[
    Flatten@Transpose[
      {#@$logU1[k, A, F], #@$logU2[k, A, F]} & /@
       {Re, Abs, Im, 
        Arg}]], {k, -Pi, Pi},
   WorkingPrecision -> 20,
   PlotStyle -> {Thick, Directive[Thick, Dashed]},
   PlotPoints -> 50,
   PlotRange -> {Automatic, {-3.5, 3.5}},
   Frame -> True,
   Axes -> False,
   PlotLegends -> {
     "Re[$logU1]", "Abs[$logU1]", "Im[$logU1]", "Arg[$logU1]",
     "Re[$logU2]", "Abs[$logU2]", "Im[$logU2]", "Arg[$logU2]"}]],
 {{a, Pi/2, "A"}, 0, 2 Pi,
  Appearance -> "Labeled"},
 {{f, Pi/2, "F"}, 0, 2 Pi, Appearance -> "Labeled"}]

enter image description here

However, there is a lot of overlap amongst the functions with both $logU1 and $logU1 plotted together. While the answer to your original question used {Re, Abs, Im, Arg}, this was to demonstrate that they could each be plotted. Normally you would pick a subset, e,g,, {Re, Im} or {Abs, Arg}, particularly with multiple functions.

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198