Find path through a set of Coordinates

Question

I have a set of coordinates that I need a robot to draw, thus it must take the shortest path along these coordinates. Plotting them looks like this:

Graphics[Point[maskCoordinates]]

EDIT: maskCoordinates is derived from the following code, which runs EdgeDetect and ComponentMeasurements on any given image, and for this example works with the first mask:

intWidth = 100;
imgCar = Import["https://2hire.io/wp-content/uploads/2016/12/car.png"];
imgCar = ColorConvert[imgCar, "Grayscale"];
imgCar = ImageResize[imgCar, intWidth];

edges = Thinning@EdgeDetect@imgCar;
masks = ComponentMeasurements[edges, "Mask"];
maskCoordinates = PixelValuePositions[Image@masks[[1, 2]], 1];

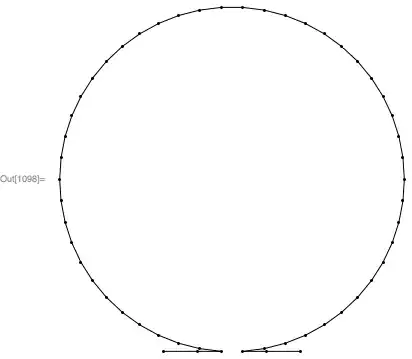
I have tried using FindShortestTour, but that only works for "complete" shapes/masks that I'm working with, like a circle. So applying this to the given mask, I get:

Graphics[Line[maskCoordinates[[Last[FindShortestTour[maskCoordinates]]]]]]

Which is close, but not exactly what I want. I thought that FindShortestPath would get the job done, but haven't had any succes with that yet.

Aren't you looking for the Nearest local point at each step, rather than the global shortest path? — aardvark2012, Oct 21 '17 at 11:58
@Androvich Your code for maskCoordinates doesn't work with the first image from the question. Please provide the explicit set of points or the original image imgCar to which the code should be applied. — Alexey Popkov, Oct 21 '17 at 12:24

Carl Woll · Answer 1 · 2017-10-21T17:01:42.457

ListCurvePathPlot is pretty close:

ListCurvePathPlot[maskCoordinates]

FindShortestTour

You can get your FindShortestTour method to work if you give FindShortestTour a good starting and ending point. For instance, we can find the left-most and right-most points using Ordering:

left = First @ Ordering[maskCoordinates, 1]
right = First @ Ordering[maskCoordinates, -1]

110

115

Feed these to FindShortestTour:

tour = FindShortestTour[maskCoordinates, left, right][[2]];

Plot the tour:

Graphics[{Line[maskCoordinates[[tour]]]}]

Update to add comparisons I think the NearestNeighborGraph and FindCurvePath approaches won't work well when the path has a near intersection that is smaller than the distance between points on the path. To show this, here is a comparison of the three current answers on such a set of points:

pts = Join[{
    {.2,-.998027},{.4,-.998026}},
    N @ CirclePoints[{0,0},1,50],
    {{-.2,-.998027}, {-.4,-.998027}
}];
Graphics @ Point @ pts

Here is the result using FindShortestTour (starting and ending points are needed for this approach):

Graphics[{
    Line @ pts[[Last @ FindShortestTour[pts, 2, 54]]],
    Point @ pts
}]

Here is the result using NearestNeighborGraph:

Graphics[{
    Line @ FindHamiltonianPath @ NearestNeighborGraph[pts, 2],
    Point[pts]
}]

The approach using FindCurvePath suggested by @AlexeyPopkov didn't work for this set of points.

ListCurvePathPlot seems quite good, but how do I get the array of coordinates as a list?
I also think that FindShortestTour might be the best option here, where I tried it with Last & First, I didn't think about using Ordering. I'll have to experiment with this as soon as I get access to the robot again - thanks a lot! — Androvich, Oct 22 '17 at 21:08

score 7 · Answer 2 · answered Oct 21 '17 at 14:57

7

Graphics @ Line @ FindHamiltonianPath @ NearestNeighborGraph[maskCoordinates, 2]

answered Oct 21 '17 at 14:57

Simon Woods

84,945
8
175
324

I think NearestNeighborGraph will not work when the path has near intersections that are smaller than the distance between points. For example, try your method with pts=Join[{{.2,-.998027},{.4,-.998026}},N @ CirclePoints[{0,0},1,50],{{-.2,-.998027},{-.4,-.998027}}]. – Carl Woll Oct 21 '17 at 16:46
@CarlWoll I agree, but can that occur when the points are pixel positions from an image edge component ? – Simon Woods Oct 21 '17 at 16:59
Since we have 8-connectivity in the original pixels, we can utilize this fact by providing radius Sqrt[2]: NearestNeighborGraph[maskCoordinates, {2, Sqrt[2]}]. – Alexey Popkov Oct 21 '17 at 18:21
Neat! I'm going to try this out as soon as I get access to the robot and see what works the best, thanks! – Androvich Oct 22 '17 at 21:10

Alexey Popkov · Answer 3 · 2017-11-13T09:55:06.440

Using a "fix" for FindCurvePath by Michael E2 from here (please read the original answer):

segments = FindCurvePath@maskCoordinates;
edges = Partition[#, 2, 1] & /@ segments;
edges = Join @@ edges;

g = Graph@edges;
path = FindShortestPath[g, ##] & @@ 
  Flatten[Position[VertexDegree[g], 1]];

Graphics[Line[maskCoordinates[[path]]]]

Looks good at first sight, but some points aren't included:

maskCoordinates // Length
path // Length
ListPlot[maskCoordinates[[#]] & /@ segments]

149
142

Some other techniques can be found in answers to the following questions:

... and in the following answers:

An interesting approach indeed, going to try it! I think that FindShortestTour with give start and end coordinates might work well, but I'm going to try all the different methods and see what works best, thank you. — Androvich, Oct 22 '17 at 21:12

Find path through a set of Coordinates

3 Answers3

Linked