Finding a Voronoi nerve

Question

I have a Voronoi mesh and I need to find a "nerve" which is all the polygons that have common edges with a specific single polygon (a nucleus). Which Mathematica functions can I use?

Answer 1

Henrik Schumacher wrote a very nice answer that provides the building blocks for converting a mesh to a graph based on the adjacency of its cells. This is now incorporated into IGraph/M.

Thus, let's build a mesh.

pts = RandomReal[1, {50, 2}];

mesh = VoronoiMesh[pts]

Load the package.

<< IGraphM`

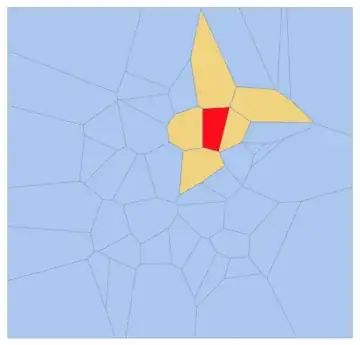
Let this be our cell of interest:

center = {2, 13};

{2, 13} means the 13th 2-dimensional cell in the mesh.

Get its adjacent cells, based on the adjacency graph:

neigh = AdjacencyList[
  IGMeshCellAdjacencyGraph[mesh, 2],
  center
  ]
(* {{2, 27}, {2, 28}, {2, 43}, {2, 45}, {2, 47}} *)

Highlight them:

HighlightMesh[mesh, {Style[center, Red], neigh}]

One more ingredient that you might need is matching up the Voronoi cells with their corresponding points:

• Site - Cell Correspondence in Voronoi Diagram obtained via VoronoiMesh