13

I want to apply non-geometric transformations to polygons etc, the goal is to have a Manipulate objects that behaves like that famous möbius transform video.

Since I was unable to apply non-geometric transformation to a polygon I went ahead and created a bunch of points in the plane and did appropriate transforms to them

(* plane region *)
region = {-1, 1};
d = 0.07;
(* Some points in plane *)
pts = Flatten[Table[{xi, yi, 0},
    {xi, First@region, Last@region, d},
    {yi, First@region, Last@region, d}]
   , 1];
col = ColorData["Rainbow"] /@ Rescale[pts[[All, 1]], region];
(** Projections from plane to sphere on line going through north pole \
of sphere centered at {0, 0, 1} **)

(* Plane to sphere )
f[vec_] := With[{t = 4/(4 + vec[[1]]^2 + vec[[2]]^2)}, vect + (1 - t) {0, 0, 2}]
(* Sphere to plane )
g[vec_] := With[{t = -(2/(-2 + Last@vec))}, vect + (1 - t) {0, 0, 2}]


rt = RotationTransform[2.1, {0, 1, 0}, {0, 0, 1}];
Graphics3D[{
  {Black, Opacity[0.3], Sphere[{0, 0, 1}]},
  Point[(rt@f@# &) /@ pts, VertexColors -> col],
  Point[((g@rt@f@# &) /@ pts), VertexColors -> col]
  },
 PlotRange -> {{-10, 10}, {-10, 10}, {0, 2}}]

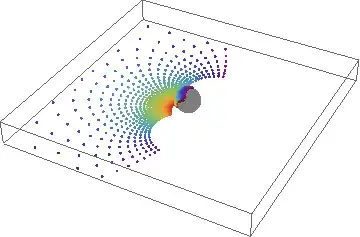
output

I wish that I could instead do something like:

Graphics3D[{
 {Black, Opacity[0.3], Sphere[{0, 0, 1}]},
 SomeTransformation[Polygon[{ {-1, -1, 0}, {-1, 1, 0}, {1, 1, 0}, {1, -1, 0}}], rt@f@#&],
 SomeTransformation[Polygon[{ {-1, -1, 0}, {-1, 1, 0}, {1, 1, 0}, {1, -1, 0}}], g@rt@f@#&]
 ]

And end up with a smooth output, not just a few points here and there.

Is there already a function like this that I have missed?

If not are there other ways to arrive at the same result?

How about for more advanced transformations?

Community
  • 1
ssch
  • 16,590
  • 2
  • 53
  • 88

3 Answers3

15

I understand that it's better to use 3D vector primitives than images at certain stages of the process. Eventually, though, everything gets rasterized, so you could just use ImageTransformation for a quick fix...

mona lisa overdrive

Manipulate[
  compiledFunction = Compile[{{x, _Real}, {y, _Real}, {fg, _Real}},
    Module[{r = x + I y},
     r = r + fg / r - fg;
     {Re[r], Im[r] }]
    ];
  ImageTransformation[img, 
   compiledFunction[#[[1]], #[[2]], s] &, 
   DataRange -> {{-1, 1}, {-1, 1}}, Padding -> "Reversed"],
  {s, -3, 3, .1}]
cormullion
  • 24,243
  • 4
  • 64
  • 133
13

Using parametrized surfaces it all becomes quite simple

σ[u_, v_] := {u, v, 0};

Manipulate[
 (* Rotations *)
 rtx = RotationTransform[ϕ, {1, 0, 0}, {0, 0, 1}];
 rty = RotationTransform[θ, {0, 1, 0}, {0, 0, 1}];
 rtz = RotationTransform[τ, {0, 0, 1}, {0, 0, 1}];
 rt = rtz@rty@rtx@# &;

 Show[
  ParametricPlot3D[{g@rt@f@σ[u, v], rt@f@σ[u, v]},
   {u, -1, 1}, {v, -1, 1}, 
   ColorFunction -> Function[{x, y, z, u, v}, 
     ColorData["Rainbow"][Rescale[u, {-1, 1}]]],
   RegionFunction -> Function[{x, y, z, u, v}, Last@rt@f@σ[u, v] < 1.999],
   ColorFunctionScaling -> False,
   PlotRange -> {{-5, 5}, {-5, 5}, {-0.001, 2}},
   Mesh -> 5],
  Graphics3D[{
    {Point[{0, 0, 2}]},
    {Gray, Opacity[0.7], Sphere[{0, 0, 1}, 0.99]}}]
  ], {θ, 0, 2 Pi}, {ϕ, 0, 2 Pi}, {τ, 0, 2 Pi}]

output

Update Fixed problem with north pole being covered

Compiling the functions give better interactivity

Clear[θ, ϕ, τ]
rtx = RotationTransform[ϕ, {1, 0, 0}, {0, 0, 1}];
rty = RotationTransform[θ, {0, 1, 0}, {0, 0, 1}];
rtz = RotationTransform[τ, {0, 0, 1}, {0, 0, 1}];
rt = rtz@rty@rtx@# &;

tosphere = Compile[{u, v, θ, ϕ, τ},
   Evaluate[FullSimplify[rt@f@σ[u, v], _ ∈ Reals]]
   , CompilationTarget -> "C",
   RuntimeOptions -> "Speed"];
toplane = Compile[{ u, v, θ, ϕ, τ},
   Evaluate[FullSimplify[g@rt@f@σ[u, v], _ ∈ Reals]]
   , CompilationTarget -> "C",
   RuntimeOptions -> "Speed"];

Manipulate[
 Show[
  ParametricPlot3D[{toplane[u, v, θ, ϕ, τ], 
    tosphere[u, v, θ, ϕ, τ]},
   {u, -1, 1}, {v, -1, 1}, 
   ColorFunction -> Function[{x, y, z, u, v}, ColorData["Rainbow"][Rescale[u, {-1, 1}]]],
   RegionFunction -> Function[{x, y, z, u, v}, Last@tosphere[u, v, θ, ϕ, τ] < 1.999],
   ColorFunctionScaling -> False,
   PlotRange -> {{-5, 5}, {-5, 5}, {-0.001, 2}},
   Mesh -> 5,
   PerformanceGoal -> "Quality"],
  Graphics3D[{
    {Point[{0, 0, 2}]},
    {Gray, Opacity[0.7], Sphere[{0, 0, 1}, 0.99]}}]
  ], {θ, 0, 2 Pi}, {ϕ, 0, 2 Pi}, {τ, 0, 2 Pi}]
LCarvalho
  • 9,233
  • 4
  • 40
  • 96
ssch
  • 16,590
  • 2
  • 53
  • 88
4

What you are looking for is GeometricTransformation, specifically the first form

GeometricTransformation[g, tfun]

where g is a graphics primitive (like Polygon) and tfun is a TransformationFunction. You will have to figure out how to turn f and g into an AffineTransform or even more likely a LinearFractionalTransform, but composing them with the rotation is easy:

t = LinearFractionalTransform[{{1, 0, 1}, {0, 1, 1}, {1, 1, 1}}]
q = RotationTransform[Pi/3]
Composition[q, t]
(*
TransformationFunction[{{1, 0, 1}, {0, 1, 1}, {1, 1, 1}}]
TransformationFunction[{{1/2, -(Sqrt[3]/2), 0}, {Sqrt[3]/2, 1/2, 0}, {0, 0, 1}}]
TransformationFunction[{
    {1/2, -(Sqrt[3]/2), 1/2 - Sqrt[3]/2}, 
    {Sqrt[3]/2, 1/2, 1/2 + Sqrt[3]/2}, {1, 1, 1}
}]
*)
ssch
  • 16,590
  • 2
  • 53
  • 88
rcollyer
  • 33,976
  • 7
  • 92
  • 191
  • I thought the whole point of the question was to do non geometric transformations (possibly non-linear)? Does GeometricTransformation take arbitrary functions? – rm -rf Dec 27 '12 at 16:42
  • @rm-rf it takes whatever can be turned into a TransformationFunction, so within the scope of a Möbius transform, then yes it can as those are called LinearFractionalTransform in mma. – rcollyer Dec 27 '12 at 16:44
  • Sadly if the TransformationFunction returned by LinearFractionalTransform is not affine GeometricTransformation gives the GeometricTransformation::nonaffine error – ssch Dec 27 '12 at 18:56
  • And FindGeometricTransform gives quite big alignment error for the transformations in question @rm-rf see above comment – ssch Dec 27 '12 at 18:59
  • @ssch well that sucks. I would have thought it could handle any TransformationFunction, otherwise I would not have suggested it. – rcollyer Dec 28 '12 at 03:06