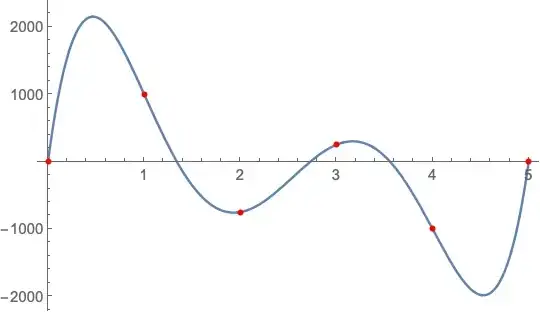
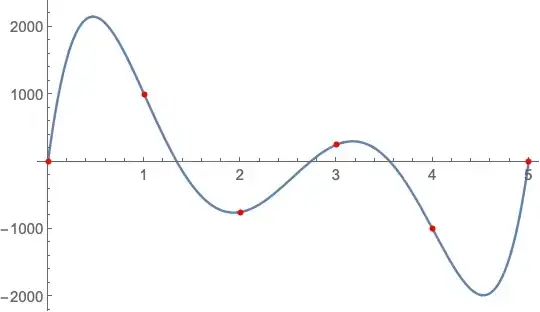
Working with other software called SolidWorks I was able to get a plot with a curve very close to my data points:
I tried to get a plot as accurate as this, but using the Fit function, I could not get a plot as accurate.
Clear["Global`*"]
dados={{0,0},{1,1000},{2,-750},{3,250},{4,-1000},{5,0}};
Plot[Evaluate[Fit[dados,{1,x,x^2,x^3,x^4,x^5,x^6},x]],{x,0,5}]
Is there something I need to modify or another method more effective than this?