I wonder what is the best practice for interpolating curves? Usually, I'm using BSplineCurve and adjusting SplineWeights so it would fit better (and assigning more weight around the sharp edges to drag the curve closer to it). Or if I can guess what formula describes the points, I use FindFit. But often, I can't guess the formula and adjusting weights is very tedious, so it's easier to just manually draw the curve along the points. So what is the best way to join points in Mathematica?
Consider these five sets of points describing five resonance curves for example:
data = {{{100.434, 0.}, {102.461, 0.0909091}, {104.392, 0.318182}, {105.321, 0.545455},
{106.226, 1.}, {107.108, 0.545455}, {107.965, 0.318182}, {109.608, 0.136364},
{111.154, 0.0909091}},
{{100.434, 0.}, {102.461, 0.06}, {104.392, 0.22}, {105.321, 0.46}, {106.226, 1.},
{107.108, 0.4}, {107.965, 0.12}, {111.154, 0.02}, {113.958, 0.}},
{{100.434, 0.030303}, {102.461, 0.0505051}, {104.392, 0.0909091},
{105.321, 0.272727}, {105.867, 0.494949}, {106.226, 1.}, {106.582, 0.636364},
{107.108, 0.212121}, {107.965, 0.0505051}, {111.154, 0.}},
{{100.434, 0.}, {102.461, 0.0555556}, {104.392, 0.333333}, {105.321, 0.611111},
{105.867, 1.}, {106.226, 0.944444}, {106.405, 0.583333}, {106.582, 0.777778},
{106.933, 1.}, {107.965, 0.444444}, {109.608, 0.166667}, {111.154, 0.0555556}},
{{100.434, 0.0188679}, {102.461, 0.0566038}, {104.392, 0.}, {105.321, 0.54717},
{105.867, 0.849057}, {106.226, 1.}, {106.405, 0.433962}, {106.582, 0.886792},
{106.933, 0.924528}, {107.281, 0.660377}, {107.965, 0.320755},
{111.154, 0.0566038}}}
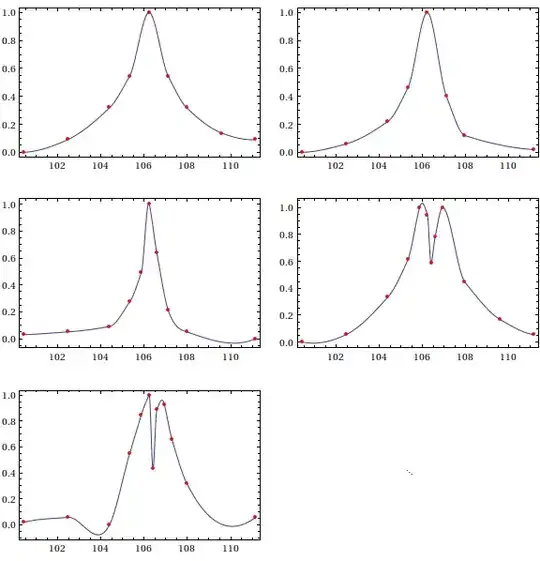




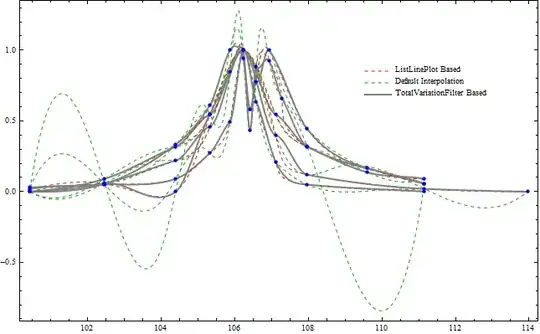

Interpolation[]? – VLC Nov 02 '12 at 16:53Method -> "Spline"it produces quite smooth curve but still not like I would join it manually. Is there a better way? – swish Nov 02 '12 at 17:07Show[ListLinePlot[#, InterpolationOrder -> 3, Method -> "Spline", PlotRange -> All, PlotStyle -> Hue[RandomReal[]], Frame -> True, Axes -> None] & /@ data, Epilog -> {Red, PointSize[Medium], Point[Flatten[data, 1]]}]how do you find the interpolation? I guess this is quite a nice interpolation as the functions are at least twice differentiable. – PlatoManiac Nov 02 '12 at 17:29ff = Interpolation[#, Method -> "Spline", InterpolationOrder -> 3] & /@ data; Plot[#[x] & /@ ff // Release, {x, 101, 111}, Epilog -> {Red, PointSize[Medium], Point[Flatten[data, 1]]}]– chris Nov 02 '12 at 18:11