FiniteElement v.s. TensorProductGrid: which is reliable for Schrödinger equation with periodic b.c.?

Question

This is a problem comes up in the discussion under this post and I think it's worth starting a new question for it.

I suspect the underlying issue is the same as in this post, but not sure.

Consider the following example:

mol[n:_Integer|{_Integer..}, o_:"Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> n, 
    "MinPoints" -> n, "DifferenceOrder" -> o}}

molfem[measure_: Automatic] := {"MethodOfLines", 
   "SpatialDiscretization" -> {"FiniteElement", 
     "MeshOptions" -> MaxCellMeasure -> measure}};

Clear@solve;
tend = 5;
solve[opt_] := 
 NDSolveValue[{I D[u[t, x], t] == -D[u[t, x], {x, 2}] + I Sin[x] u[t, x], 
   u[0, x] == Exp[-x^2] Exp[I x], u[t, -Pi] == u[t, Pi]}, u, {t, 0, tend}, {x, -Pi, Pi}, 
  Method -> opt]

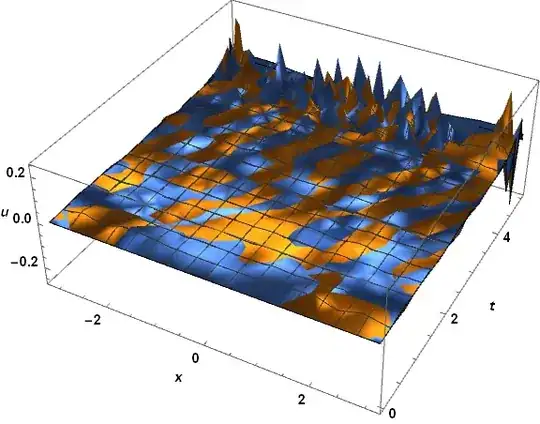
soltraditional = solve@mol[200, 4]
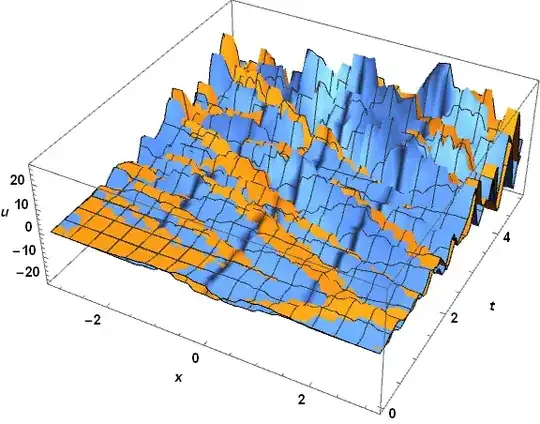
solfem = solve@molfem[]

Plot[{ReIm@solfem[tend, x], ReIm@soltraditional[tend, x]}, {x, -π, π}]

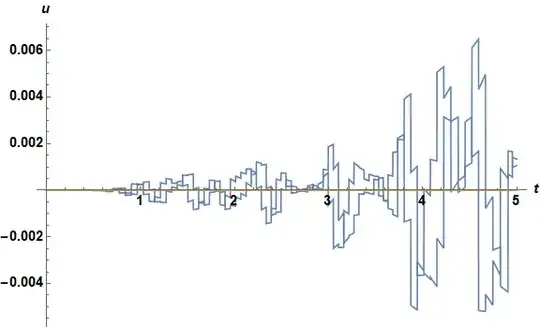
Plot[{Abs@solfem[tend, x], Abs@soltraditional[tend, x]}, {x, -π, π}]

The difference is obvious.

Which solution is the reliable one?

Answer 1

Plugging the solutions into the PDE yields for soltraditional

(I D[u[t, x], t] + D[u[t, x], {x, 2}] - I Sin[x] u[t, x]) /. u -> soltraditional;
Plot3D[Evaluate@ReIm@%, {x, -Pi, Pi}, {t, 0, tend}, PlotRange -> All, 
    ImageSize -> Large, AxesLabel -> {x, t, u}, LabelStyle -> {Bold, Black, 15}]

which is not so good, the spiky behavior near t == tend suggesting the onset of instability. In contrast, the result for solfem is simply terrible, as though it were the solution of a different PDE!

The discrepancies are not associated particularly with the boundary conditions, suggesting that the problem here is not the same as in the second post mentioned in the question.

Plot[{ReIm@(solfem[t, Pi] - solfem[t, -Pi]), 
      ReIm@(soltraditional[t, Pi] - soltraditional[t, Pi])}, {t, 0, tend},
      PlotRange -> All, ImageSize -> Large, AxesLabel -> {t, u}, 
      LabelStyle -> {Bold, Black, 15}]

To answer the specific question posed by the OP, soltraditional is much more credible than solfem.

Addendum: Solutions with potential eliminated

Repeating these computations with the term I Sin[x] u[t, x] eliminated from the PDE yields somewhat similar results. The soltraditional solution is noisy but now shows no sign of instability. The solfem solution again does not satisfy the PDE.

At least superficially, this looks like a bug.