Filling and Shading an Harmonic Curve

Question

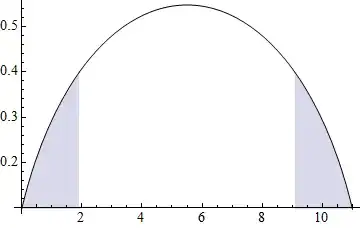
Suppose I have an equation plotted as shown:

Plot[(HarmonicNumber[K] - HarmonicNumber[K - r]) (HarmonicNumber[K] - 
 HarmonicNumber[-1 + r]) /. K -> 10, {r, 0, 11}, Filling -> 0.4]

But what I really want is to have the two (triangular?) filling FLIPPED inside at $x \approx2$ and $x \approx9$. The direction of filling of the upper (semi-circular) part is not important. Preferably it can be Top/outside.

Can anybody help with this flipping?

Thanks

Related: (9684), (14696), (18964), (25169) – Mr.Wizard May 22 '13 at 08:42 — Mr.Wizard, May 22 '13 at 08:42

score 6 · Accepted Answer · edited Apr 13 '17 at 12:55

Another way, copying once more from @J.M.'s answer here: How can I fill under a function in a plot just to right of a specified vertical line?

Using @b.gatessucks definition of f:

f[r_, k_] = (HarmonicNumber[k] - HarmonicNumber[k - r]) (HarmonicNumber[k] - 
      HarmonicNumber[-1 + r])

we can do:

With[{ff = f[r, 10]}, 
   Plot[{ConditionalExpression[ff, ff < 0.4], 
         ConditionalExpression[ff, ff >= 0.4]}, {r, 0, 11}, 
   Filling -> {1 -> Axis, 2 -> Top}, PlotStyle -> ColorData[1, 1], 
   FillingStyle -> LightRed]]

based on the ideas linked above (using ConditionalExpression), getting the same result as in @b.gatessucks' answer.

The advantage of this approach is that you can easily modify the fillings (and other options) for the individual parts (but if you use a complicated function, I suspect it could turn slow (due to the added conditions)

score 5 · Answer 2 · answered May 22 '13 at 08:21

One way :

f[r_, k_] = (HarmonicNumber[k] - HarmonicNumber[k - r]) (HarmonicNumber[k] - 
 HarmonicNumber[-1 + r])

sol1 = r /. FindRoot[f[r, 10] == 0.4, {r, 2}];
sol2 = r /. FindRoot[f[r, 10] == 0.4, {r, 9}];
m = FindMaximum[f[r, 10], {r, sol1, sol2}][[1]];

Show[Plot[f[r, 10], {r, 0, 11}], 
     Plot[f[r, 10], {r, 0, sol1}, Filling -> Bottom], 
     Plot[f[r, 10], {r, sol1, sol2}, Filling -> {1 -> m}], 
     Plot[f[r, 10], {r, sol2, 11}, Filling -> Bottom]]

enter image description here

score 4 · Answer 3 · answered May 22 '13 at 09:18

You could draw an invisible second function (a block) and have the filling occur between the two:

f[r_, k_] = (HarmonicNumber[k]-HarmonicNumber[k-r])(HarmonicNumber[k]-HarmonicNumber[-1 + r]);

max = NMaxValue[{f[r, 10], 0 < r < 11}, r]
min = NMinValue[{f[r, 10], 0 <= r <= 11}, r]

Plot[
  {
    f[r, 10], 
    Rescale[ Boole[f[r, 10] > 0.4], {0, 1}, {min, max}]
  }, 
  {r, 0, 11}, 
  Filling -> {1 -> {2}}, 
  PlotStyle -> {Automatic, None}
]

enter image description here

Thanks all. You been quite helpful. – Afloz May 22 '13 at 09:54 — Afloz, May 22 '13 at 09:54

Mr.Wizard · Answer 4 · 2013-05-22T09:02:58.883

For version 7:

Warning: for simplicity r is not localized in either method; Formal Symbols advised in practice.

hf[K_] := With[{H = HarmonicNumber}, (H[K] - H[K - r]) (H[K] - H[r - 1])]

Plot[
 {If[hf[10] < 0.4, hf[10]], If[hf[10] >= 0.4, hf[10]]},
 {r, 0, 11}, 
 Filling -> {1 -> Bottom},
 PlotStyle -> Black
]

enter image description here

Or:

Plot[
 {If[hf[10] < 0.4, hf[10]], If[hf[10] >= 0.4, hf[10]]},
 {r, 0, 11}, 
 Filling -> {1 -> Bottom, 2 -> Top},
 FillingStyle -> LightGray,
 PlotStyle -> Black
]

enter image description here

Filling and Shading an Harmonic Curve

4 Answers4

Linked