3
In[1]:= Level[1/2,{-1}]
Out[1]= {1/2}

TreeForm[1/2]

enter image description here

In[2]:= Level[1/2,{-1}]
Out[2]= {1/2}

In[3]:= Level[Unevaluated[1/2],{-1}]
Out[3]= {1,2,-1}

In[4]:= 1/2//FullForm
Out[5]//FullForm= Rational[1,2]

Rational[1,2] in TreeForm,but Times[1,Power[2,-1]] when Level.

In[5]:= Level[Unevaluated[1/2],{-1},Heads->True]
Out[5]= {Times,1,Power,2,-1}

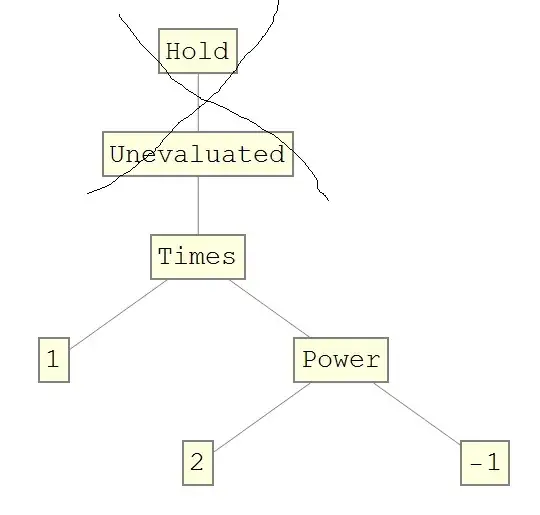
How to comprehend this? How to obtain TreeForm[Hold@Unevaluated[1/2]] without Hold and Uevaluated in whole TreeForm's graph or TreeForm@{{{Hold[1/2],b}},b,c} with out hold? enter image description here

And How to get {1,2} from Level[1/2, {-1}]?

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
HyperGroups
  • 8,619
  • 1
  • 26
  • 63

1 Answers1

2

There is an evaluation leak in TreeForm that requires a double-Unevaluated to circumvent:

TreeForm[Unevaluated @ Unevaluated[1/2]]

enter image description here

The second question is more troublesome. Because Rational is an atomic object Level does not extract its conceptual sub-parts. This is true of other atomic objects as well:

sa = SparseArray @ Range @ 5;
Level[sa, {-1}]

{SparseArray[<5>,{5}]}

The only thing I can think of is a conversion to held FullForm as follows:

Level[MakeExpression @ ToBoxes @ FullForm[1/2], {-1}]

{1, 2}

Level[MakeExpression @ ToBoxes @ FullForm[sa], {-1}]

{Automatic, 5, 0, 1, 0, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5}
Community
  • 1
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • {Numerator[1/2], Denominator[1/2]} seems a more straightforward way to get the parts, unless one insists on using Level – Aky May 23 '13 at 12:19
  • @Aky I interpret the question as specifically "insisting on Level" rather than generically splitting a Rational object; I think Rational is only one example. – Mr.Wizard May 23 '13 at 12:22
  • @MrWizard That makes sense. When I wrote that, I hadn't realised that your technique could be used with other atomic expressions too. Thanks for clarifying. – Aky May 23 '13 at 12:27
  • @MrWizard Is there any advantage to using ToBoxes vs. ToString? (I don't actually know anything about "boxes" yet, but just asking.) – Aky May 23 '13 at 12:28
  • @Aky I updated my answer to make that more apparent. I changed from using ToString to ToBoxes because the latter should be more robust: any expression can be represented in Box form while certain things may be changed/lost in the string conversion. – Mr.Wizard May 23 '13 at 12:30
  • ha, I think this should be researched by someone before, you did it, I never thought I would use two Unevaluated before. – HyperGroups May 24 '13 at 02:56
  • @Aky as Mr.Wizard said, Numberater[1/2+a] would be failed, for this is an generic question rather than the case 1/2. – HyperGroups May 24 '13 at 02:58
  • @HyperGroups yeah I got that now, thanks ;) – Aky May 24 '13 at 09:44
  • @HyperGroups see Leonid's comments under the StackOverflow post I linked. One Unevaluated should have been sufficient but somewhere in TreeForm there is an evaluation leak which is stopped by the inner Unevaluated. – Mr.Wizard May 24 '13 at 13:23