Unevaluated @ {args} versus Unevaluated /@ {args}

Question

Working my way through Robby Villegas's lovely notes on withholding evaluation, I almost got Polish Notation on my first try. Here is my final solution, which seems to work well enough:

ClearAll[lispify];
SetAttributes[lispify, HoldAll];
lispify[h_[args___]] :=
  Prepend[
   lispify /@ Unevaluated @ {args},
   lispify[h]];
lispify[s_ /; AtomQ[s]] := s;

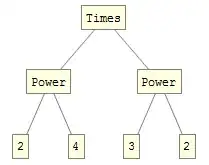
lispify[Unevaluated[2^4 * 3^2]]

produces

{Times, {Power, 2, 4}, {Power, 3, 2}}

My first try had only one difference, namely

lispify /@ Unevaluated /@ {args}

and sent me down a frustrating rabbit hole until I stumbled on the corrected one above.

Would someone be so kind as to explain the details of both the correct and incorrect solution?

EDIT:

As a minor bonus, this enables a nice way to visualize unevaluated expression trees:

ClearAll[stringulateLisp];
stringulateLisp[l_List] := stringulateLisp /@ l;
stringulateLisp[e_] := ToString[e];
ClearAll[stringTree];
stringTree[l_List] := First[l][Sequence @@ stringTree /@ Rest[l]];
stringTree[e_] := e;
ClearAll[treeForm];
treeForm = TreeForm@*stringTree@*stringulateLisp@*lispify;
treeForm[Unevaluated[2^4 + 3^2]]

Mathematica graphics

thank you for having the forethought of kindly sharing a link to Vellega's notes notebook about controlling evaluation from a 1999 conference. ive been looking for something like this nearly my entire short wolfram life. although somewhat dated pretty much all of it is still relevant today. :) — Jules Manson, Apr 05 '22 at 07:06

score 8 · Accepted Answer · edited Apr 13 '17 at 12:55

You must remember that Unevaluated only "works" when it is the explicit head of an expression. In the non-working format the structure looks like:

TreeForm @ HoldForm[lispify /@ Unevaluated /@ {arg1, arg2}]

enter image description here

Note that Unevaluated does not surround arg1 and arg2 therefore they evaluate prematurely.

Now compare the working structure:

TreeForm @ HoldForm[lispify /@ Unevaluated @ {arg1, arg2}]

enter image description here

Here Unevaluated does surround arg1 and arg2 and evaluation is prevented.

Unevaluated @ {args} versus Unevaluated /@ {args}

1 Answers1

Linked