I have the following Mathematica code:
$Assumptions = {r \[Element] Reals, r >= 0, rh \[Element] Reals,
rh > 0};
S[rh_] := \[Pi] rh^2
M[rh_, qe_, qm_] :=
1/2 Sqrt[\[Pi]/S[rh]] (S[rh]^2/\[Pi]^2 + S[rh]/\[Pi] + qe^2 + qm^2)
qe = SolveValues[\[Phi]e == qe (1/rh - 1/r), qe];
f[r_, rh_, qm_, \[Phi]e_] :=
1 + r^2/l^2 - (2 M[rh, qe, qm])/r + (qe^2 + qm^2)/r^2
G[rh_, qm_, \[Phi]e_] :=
1/(4 \[Pi]^2) Sqrt[\[Pi]/
S[rh]] (3 \[Pi]^2 qm^2 - S[rh]^2 + \[Pi] S[rh] (1 - \[Phi]e^2))
T[rh_, qm_, \[Phi]e_] := (-\[Pi]^2 qm^2 +
3 S[rh]^2 + \[Pi] (S[rh] - S[rh] \[Phi]e^2))/(4 (\[Pi] S[rh])^(3/2))
Veff[r_] := f[r, rh, qm, [Phi]e] (L^2/r^2 + 1);
eqn = L^2 == (r0^3 D[f[r0, rh, qm, [Phi]e],
r0])/(2 f[r0, rh, qm, [Phi]e] -
r0 D[f[r0, rh, qm, [Phi]e], r0]) /. r -> r0 // Simplify
sol = Block[{l = 1, L = 20, [Phi]e = 0.6}, Solve[eqn, r0, Reals]]
l = 1; L = 20; [Phi]e = 0.6;
[Lambda][rh_, qm_, [Phi]e_] =
1/2 Sqrt[(r0 D[f[r0, rh, qm, [Phi]e], r0] -
2 f[r0, rh, qm, [Phi]e]) Veff''[r0]] /. r -> r0 /.
sol[[5]] // Simplify;
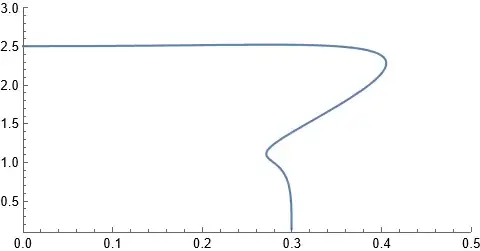
pplt1 = ParametricPlot[{T[rh, 0.05, [Phi]e], [Lambda][rh,
0.05, [Phi]e]}, {rh, 0.01, 2}, PlotRange -> {{0.1, 0.4}, {0, 2}},
AspectRatio -> 0.5]
which gives me the following plot as the output:
while the desired plot should look similar to this:
How to resolve this issue?