6

I want to solve two coupled equations with NDSolve,

t x'[t] == -x[t] + y[t], t y'[t] == -5 t^2/x[t]^2 + x[t] - y[t], 
x[0] == y[0], x[1] == 1

It's easy to see that at t = 0 the derivative is undetermined, so NDSolve fails.

The Mathematica help center told me one possibility is to start at a small ε > 0 instead of 0, and another possibility is to use the option SolveDelayed -> True to avoid the singularity in the solved form of the equations.

Unfortunately neither of the methods worked for me. What should I do?

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
3c.
  • 669
  • 1
  • 7
  • 13

1 Answers1

13

You can try "shooting method":

eqn1 = t x'[t] - (-x[t] + y[t]);
eqn2 = t y'[t] - (-5 t^2/x[t]^2 + x[t] - y[t]);
sol = NDSolve[{eqn1 == 0, eqn2 == 0, x[0] == y[0], x[1] == 1}, {x, y}, {t, 0, 1}, 
              Method -> {"Shooting", "StartingInitialConditions" -> 
                                     {x[1] == 1, y[1] == 2/100 + 91/16000}}];
Plot[{x[t], y[t]} /. sol, {t, 0, 1}, Evaluated -> True]

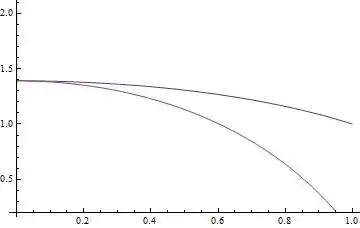
enter image description here

The "StartingInitialConditions" above is found by trial and error, despite some warnings generated, the solution is reliable enough:

(* Error check *)
Plot[{eqn1, eqn2} /. sol, {t, 0, 1}, Evaluated -> True]
Plot[{eqn1, eqn2} /. sol, {t, 0, 1}, PlotRange -> All]

enter image description here enter image description here

Edit

Let me add some explanations about how I found a good initial condition. As I've mentioned in the comment below, what I used is just method of exhaustion… yeah, exhaustion, sounds clumsy but it's really powerful.

First, I define the following function for the realization of the method:

ClearAll[try]
SetAttributes[try, Listable]
try[i_] :=(* try[i] = *){i, Quiet@NDSolve[{eqn1 == 0, eqn2 == 0, x[0] == y[0], x[1] == 1}, 
                           {x, y}, {t, 0, 1}, Method -> {"Shooting", 
                           "StartingInitialConditions" -> {x[1] == 1, y[1] == i}}]};

If you add the try[i] = in the note into the code, Mathematica will remember all the calculated try[i] so repetitive computation can be avoided when rechecking, of course this will consume more memory and not that necessary for your case.

We don't know what value will be a proper initial condition, but it's not that hard to guess the approximate extent of it, based on some observations to the equations and boundary conditions, I guess that y[1] may be between -10 and 10. So I tried:

midpoint = 0; step = 1; 
try@Range[midpoint - 10 step, midpoint + 10 step, step] // MatrixForm

enter image description here

All of the trials fail in the middle of the domain of t, but one of them stick out to about 0.02, with y[1] == 0, which means a proper initial condition may be near 0, so I go on trying:

midpoint = 0; step = 1/10; 
try@Range[midpoint - 9 step, midpoint + 9 step, step] // MatrixForm

enter image description here

The best condition we found is still y[1] == 0 but the scope is smaller now… wait, so far I was modifying midpoint and step by hand, why not make them modified automatically?:

Clear[leftboundary, area]
(* leftboundary is used for the extraction 
   of the left boundary of the interpolating function,
   it's specifically designed for the structure of try[i]. *)
leftboundary = First@First@First@First[x /. Last@#] &;
(* area is used for the generation of possible y[1] *)
area[midpoint_, step_] := Range[midpoint - 9 step, midpoint + 9 step, step]

NestWhile[{First@SortBy[try@area[First@#, #2], leftboundary], #2/10} & @@ # &, 
          {try[0], 1/100}, leftboundary@First@# > 10^-16 &]

{513/20000, 1.24278*10^-128, 1/1000000}

OK, this time we get a even better initial condition: y[1] == 513/20000.

xzczd
  • 65,995
  • 9
  • 163
  • 468
  • 1
    by the way, do you have any idea to guess the initial condition, I tried many times, but still can not find such good initial values. thanks – 3c. Jul 17 '13 at 14:12
  • 1
    @user8583 What I used is just method of exhaustion… of course, this can be done automatically with the combination of Table and Nest, for this part I can add something to my answer tomorrow, but now I'd like to go to bed. :D – xzczd Jul 17 '13 at 15:15
  • by the way. For your last paragraph which is talking about how to make the search automatically, I am not quite understanding what it means. such as the definition of g and the content inside nestwhile. if you have time, I appreciate your help. – 3c. Jul 22 '13 at 14:16
  • @user8583 Oh, that's a combination of "pure function" and "list manipulation", which are two of the most important parts of the core language of Mathematica, you can have a look at the documents of Function and those about list manipulation. Also, you can read through this post. If you still feel confused after check all these pages, I don't mind to add more explanations to my answer… – xzczd Jul 22 '13 at 15:14
  • I am trying to understand your last paragraph about how to search the initial condition automatically, would you mind dividing it into a simpler way? sorry for that, thanks – 3c. Oct 18 '13 at 18:30
  • @3c. I've changed the last part of the code, I think it's easier to understand now. Feel free to ask if you still feel it obscure. – xzczd Oct 19 '13 at 08:31
  • thanks, but I am still confused with what's #[[1]], and #[[2]], for your last code, which is nestwhile, {First@SortBy[f@h[First@#[[1]], #[[2]]], g], #[[2]]/10} & acts on {f[0], 1/100}, which means f@h[First@#[[1]], #[[2]]], g] acts on f[0], and #[[2]]/10 acts on 1/100, I am confused. could you explain it more clearly? – 3c. Oct 20 '13 at 23:28
  • @3c. you seem to misunderstand the syntax of NestWhile, for the first round of iteration, # in the first argument means the second argument of NestWhile i.e. #[[1]] represents {f[0], 1/100}[[1]], #[[2]] represents {f[0], 1/100}[[2]] so the calculated expression is {First@SortBy[f@h[First@f[0], 1/100], g], 1/100/10}. – xzczd Oct 21 '13 at 05:09
  • that's where my confusion. Thank you. By the way, because you notice the initial condition is around i=0, what if you do not know that, can you start from any i and find the right initial value? – 3c. Oct 21 '13 at 19:23
  • @3c. I'm sorry that I can't think out a efficient algorithm which can start from any i so far… But also notice that the rough range for the current algorithm can be quite extensive. (What I used is $[-10, 10]$ at beginning.) – xzczd Oct 22 '13 at 02:31
  • thanks anyway. my current problem is for any boundary point instead of 0, I need to find the initial condition i. I have no idea to figure it out – 3c. Oct 22 '13 at 14:44