- I am new to Mathematica and would like to find the set $$\{ (x,y) \in \mathbb{R}^2: (3x+y\exp(xy))(x-a) + (6y + x \exp(xy))(y-b) < 0 \}$$ for some constants $a$ and $b$. How can I do this? Added: Is the set empty when a=-1.0643 and b=0.150?
- My actual question may be more difficult. For this function $f:\mathbb{R}^2 \to \mathbb{R}$, defined as $$ f(x,y) := (3x+y\exp(xy))(x-a) + (6y + x \exp(xy))(y-b) $$ I would like to know its range $f(\mathbb{R}^2)$, or better yet $f(\mathbb{R}^2 - \{(a,b)\})$, or as close as possible. Can it be done in Mathematica as well?
2 Answers
[Please please please...post actual cut-and-pastable code.]
Here is a method that is, unfortunately, impractical. But it sometimes gives results if you are patient.
isEmpty[a_?NumericQ, b_?NumericQ] := Module[{finst},
finst =
FindInstance[(3*x + y Exp[x*y])*(x \[Minus] a) + (6*y +
x*Exp[x*y])*(y \[Minus] b) < 0, {x, y}];
If[ListQ[finst],
If[Length[finst] == 0, True, False]
, $Failed]
]
In[306]:= isEmpty[1, 3]
Out[306]= False
Here is a start on a method that uses contpur plotting. One must settle for a finite range on {x,y} for this; I use -+10 for both.
isEmpty2[a_?NumericQ, b_?NumericQ] := Module[{cplot},
cplot =
ContourPlot[(3*x + y Exp[x*y])*(x \[Minus] a) + (6*y +
x*Exp[x*y])*(y \[Minus] b) == 0, {x, -10, 10}, {y, -10, 10},
ContourShading -> False, Frame -> None]
]
It just gives a picture but i guess those better versed in Mathematica's Graphics might be able to extract at True/False therefrom. It would of course not be a guaranteed resutl, since plotting uses numeric approximation methods.
It gives a nice result for a=-4, b=-1.

--- edit ---
A comment asks about a specific set of inputs for {a,b}. Not one to duck such a test, I'll show a result with FindRoot. Here we find an {x,y} pair for which the expression of interest is negative (equal to -0.2), by setting y first to 0. I did this because the contour plot indicated there was a negative region in that general vicinity.
In[339]:= FindRoot[((3*x + y Exp[x*y])*(x - a) + (6*y +
x*Exp[x*y])*(y - b) /. {a -> -1.0643, b -> -.15,
y -> 0.}) == -.2, {x, .1}]
Out[339]= {x -> -0.0634401}
--- end edit ---
- 20,779
- 2
- 64
- 121
- 58,970
- 2
- 101
- 199
-
-
@Tim No, not empty. isEmpty2[1.0643, .15] indicates a small ovaline contour. Or something. (I don't suppose "ovaline" is a word.) – Daniel Lichtblau Mar 13 '12 at 22:12
-
@Daniel: a is negative. If it is nonempty, could you give an element of the set? – Tim Mar 13 '12 at 22:13
-
-
@DanielLichtblau: Thanks! (a is negative and b positive). May I ask what "In[306]:= isEmpty[1, 3]" and "Out[306]= False" mean? Is the first one run the function isEmpty and return the false, true or failed value to the variable In[306]? What does 306 mean in both? – Tim Mar 13 '12 at 22:38
-
@Tim (I'll get it right eventually.) When b is +0.15 I get a root x -> -0.0706475. The In[306]/Out[306] is just Mathematica's way of denoting a computational input and evaluated result. – Daniel Lichtblau Mar 13 '12 at 22:42
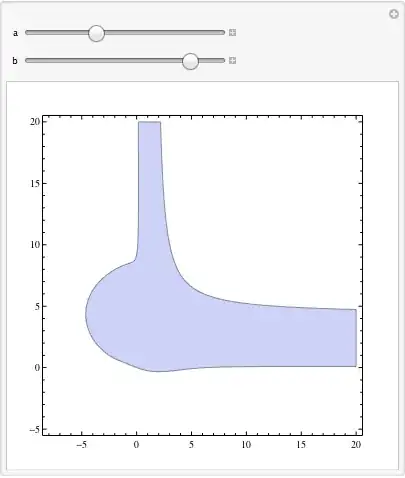
To get an indication of the region where your function is negative you could use RegionPlot. For example
ineq[x_, y_, a_, b_] :=
((3 x + y Exp[x y]) (x - a) + (6 y + x Exp[x y]) (y - b))
Manipulate[
Show[RegionPlot[ineq[x, y, a, b] < 0, {x, -8, 20}, {y, -5, 20},
ImagePadding -> 20, PlotPoints -> 30]],
{a, 0, 10},
{b, 0, 10}]
- 35,858
- 3
- 108
- 157
http://reference.wolfram.com/mathematica/ref/FindInstance.html?q=FindInstance&lang=en
If the set is not finite, then please clarify what you mean by "finding the set".
– Searke Mar 13 '12 at 21:47