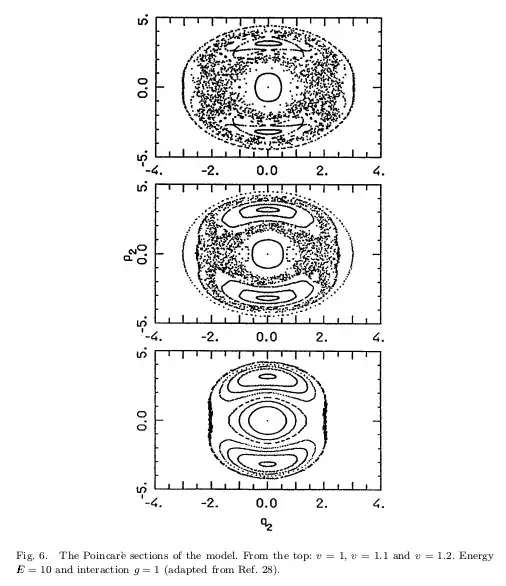
In the papers Quantum Chaos in a Yang-Mills-Higgs System and DIFFERENT FACETS OF CHAOS IN QUANTUM MECHANICS, the authors have plotted three Poincaré sections for different values of v.
I have been trying to reproduce these sections; however, they are not coming exactly. The following is my code, which I borrowed from this answer.
Hamiltonian is given by
H[px_, py_, x_, y_] := 1/2 (px^2 + py^2) + g^2*v^2*(x^2 + y^2) + 1/2*g^2*x^2*y^2
Values of parameters
g = 1; v = 1.0(*1.1*)(*1.2*);
Hamiltonian EOMs
{a1, b1, c1, d1} = {D[H[px[t], py[t], x[t], y[t]], px[t]],
D[H[px[t], py[t], x[t], y[t]], py[t]],
-D[H[px[t], py[t], x[t], y[t]], x[t]],
-D[H[px[t], py[t], x[t], y[t]], y[t]]}
n = 140;
list = Range[n];
For[i = 1;, i < n + 1, i++,
ics = {Random[Real, {-0.55, 0.55}], Random[Real, {-0.45, 0.45}],
Random[Real, {-0.44, 0.9}], Random[Real, {-0.17, 0.9}]};
inisol = Solve[H[ini, ics[[4]], ics[[1]], ics[[2]]] == 0.866, ini];
inival = ini /. inisol;
ics = {ics[[1]], ics[[2]], inival[[2]], ics[[4]]};
TimeMin = 0;
TimeMax = 1000;
Section =
Reap[NDSolve[{x'[t] == a1, px'[t] == c1, y'[t] == b1, py'[t] == d1,
x[0] == ics[[1]], y[0] == ics[[2]], px[0] == ics[[3]],
py[0] == ics[[4]]}, {x[t], y[t], px[t], py[t]}, {t, TimeMin,
TimeMax}, MaxSteps -> [Infinity],
Method -> {"EventLocator", "Event" -> x[t],
"EventAction" :> Sow[{y[t], py[t]}]}]][[2]];
list[[i]] =
ListPlot[Transpose[Table[Section, {j, Length[Section]}]][[1]][[1]],
PlotStyle -> {RGBColor[Random[], Random[], Random[]],
AbsolutePointSize[0.5]}]]
Show[list, PlotRange -> All, Frame -> True, Axes -> False,
ImageSize -> Large, LabelStyle -> Directive[White, Small],
Background -> GrayLevel[0.1]]
Another Method
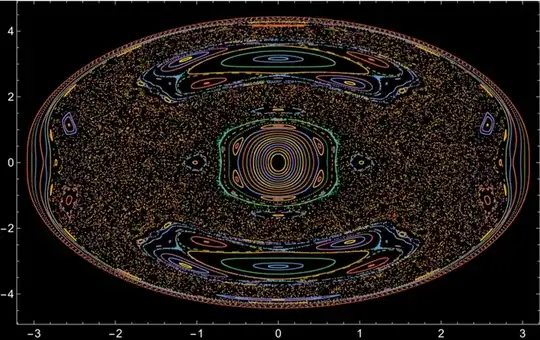
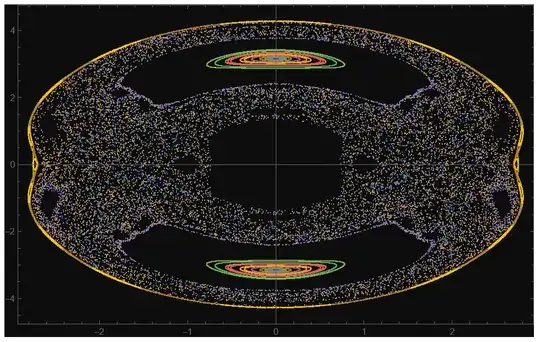
With this code, I get a different result
With[{icv = {{0, 0.4082401254164024`, 0, 0}, {0, 0.24008038662195985`, -0.15316368171208566`, 0.28838672839135326`}, {0, 0.24352018790129148`, 0.09848498536170303`, 0.3135210500944904`}, {0, 0.20788819727584018`, 0.18687849877360435`,
0.3047456328865395`}, {0, 0.11124773284074371`, 0.24234454959281115`, 0.32410152798705066`}, {0, 0.09612790055948518`, 0.2562151235263743`, 0.32091473672760257`}, {0, 0.14504873906640348`, 0.2433184249171519`, 0.3098719090788399`}, {0, 0.21466692008332666`, 0.21341797098009158`, 0.2855018063099425`}, {0, 0.2242200636897092`, 0.21057030870037158`, 0.27976766448196655`}, {0, 0.3683386516212832`, 0.18778901046261137`, 0.011696534024095057`}, {0, 0.3451153373835715`, 0.23762310035771178`, 0.005962392196119196`}, {0, 0.33504538978074816`, 0.256132905175892`, 0.0016617858251372995`}, {0, 0.37097564355830726`, -0.03575247849541091`, 0.1665183633794433`}, {0, 0.37507484064199426`, -0.06280527015275122`, 0.14788240243852177`}, {0, 0.3774580162329546`, -0.08416273725065143`, 0.12924644149760023`}, {0, 0.3779249463635693`, -0.09982487978911159`, 0.11491108692766056`}, {0, 0.3818158505457779`, -0.10979169776813169`,
0.08910744870176919`}, {0, 0.3850735819245613`, -0.11406319118771174`,
0.06617088138986574`}, {0, 0.3571135001050445`, -0.02151416709681081`,
0.1966226079763166`}, {0, 0.3537329768656702`, -0.0015805311387706023`,
0.20379028526128642`}}},
psection =
Reap[Table[
NDSolve[{x'[t] == px[t],
px'[t] == -(2 g^2 v^2 x[t] + g^2 x[t] y[t]^2), y'[t] == py[t],
py'[t] == -(2 g^2 v^2 y[t] + g^2 x[t]^2 y[t]),
x[0] == Part[icv[[i]], 1], px[0] == Part[icv[[i]], 2],
y[0] == Part[icv[[i]], 3], py[0] == Part[icv[[i]], 4]}, {x,
px, y, py}, {t, 0, 1000}, MaxSteps -> \[Infinity],
Method -> {"EventLocator", "Event" -> x[t],
"EventAction" :> Sow[{y[t], py[t]}]}], {i, 1,
Length[icv]}]][[2]];]
ListPlot[psection, PlotRange -> All, PlotTheme -> "Scientific",
LabelStyle -> Directive[Black, 18],
FrameLabel -> {{"!(*SubscriptBox[(p), (y)])", None}, {"y",
"YMH system"}}, RotateLabel -> False,
Epilog -> {Text["E=10", {0.3, 0.4}]}, ImageSize -> 400]
I think there is a problem in defining the energy surface.





{-0.45, 0.45}. Increase this range (also for $p_2$). (2) You look at $E=0.866$ (why?), when the original plots are for $E=10$. After fixing (1) and (2), you should get the correct image. – Domen Sep 14 '23 at 15:25Solve) such that the energy is what you want. You can just discard these, or, for example, choose only two initial values ($y$ and $p_y$), then calculate the relationship between the other two such that the total energy is satisfied, then pick random one satisfying the condition. – Domen Sep 14 '23 at 21:11