I am trying to recreate the Poincaré sections given in Figure 2 of this paper.

For this purpose, I use the following two methods:
Method1: Using ResourceFunction["ClickPoincarePlot2D"]
f = 2 k x[t];
lagrangian = -Sqrt[f - x'[t]^2/f - y'[t]^2] - [Omega]^2/
2 ((x[t] - xc)^2 + y[t]^2);
px1 = D[lagrangian, x'[t]]
py1 = D[lagrangian, y'[t]]
testham = (px1 x'[t] + py1 y'[t]) - lagrangian
k = 1/2; [Omega] = 10; xc = 1;
hamiltonian[x_, px_, y_, py_] =
testham /. x[t] -> x /. x'[t] -> px /. y[t] -> y /. y'[t] -> py;
H := Function[{S}, (2 k S[[1]])/Sqrt[
2 k S[[1]] - S[[2]]^2/(2 k S[[1]]) - S[[4]]^2] +
1/2 (S[[1]]^2 + S[[3]]^2 - 2 S[[1]] xc + xc^2) [Omega]^2]
{a1, b1, c1, d1} = {D[hamiltonian[x[t], px[t], y[t], py[t]], px[t]],
D[hamiltonian[x[t], px[t], y[t], py[t]],
py[t]], -D[hamiltonian[x[t], px[t], y[t], py[t]], x[t]], -D[
hamiltonian[x[t], px[t], y[t], py[t]], y[t]]}; abcd = {x'[t] ==
a1, px'[t] == c1, y'[t] == b1, py'[t] == d1};
cross = y[t]; recover = {x[t], px[t]};
ResourceFunction[
"ClickPoincarePlot2D"][abcd, H, 15, t, 10000, cross, recover, \
{PlotStyle -> AbsolutePointSize[1], AspectRatio -> 1,
PlotHighlighting -> None, PlotRange -> {{0, 2}, {-20, 20}}}]
Method2: Using algorithm of this answer by @Alex Trounev
psect[{x0_, px0_, y0_, py0_}] :=
Reap[NDSolve[{abcd, x[0] == x0 + 10^-10, y[0] == y0, px[0] == px0,
py[0] == py0, WhenEvent[x[t] == 0, Sow[{y[t], py[t]}]]}, {}, {t,
0, 1000}, MaxSteps -> \[Infinity]]][[-1, 1]]
inivalues[E0_, n_, pxmin_, pxmax_] :=
Module[{x, px, X, y, P, py, Y}, px = RandomReal[{pxmin, pxmax}, n];
X = Table[0, {n}]; Y = Table[0, {n}]; P = Table[0, {n}];
Do[{X[[i]], P[[i]], Y[[i]]} = {x, py, y} /.
NMinimize[(hamiltonian[x, px[[i]], y, py] - E0)^2, {x, py,
y}][[2]];, {i, n}]; Transpose[{X, px, Y, P}]];
iniv = inivalues[15, 100, -0.1, 0.1];
H0[{x_, px_, y_, py_}] = -Sqrt[f - px^2/f - py^2] - [Omega]^2/
2 ((x - xc)^2 + y^2) + px^2 + py^2;
abcdata = Map[psect, iniv];
ListPlot[abcdata, ImageSize -> Large, Background -> White,
Frame -> True]
I tried to alter the cross and recover variables in both methods but to no avail! The first method gives me an empty plot while the second one provides me with errors!
Any help in this regard would be truly beneficial!

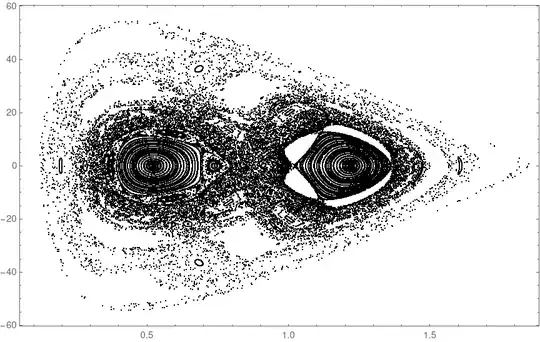










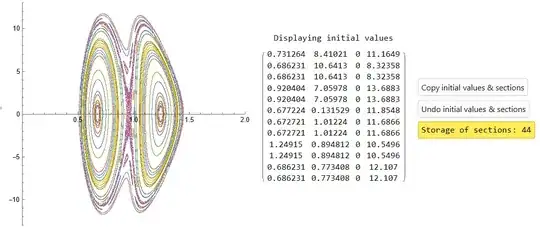


ClickPaneand post it as an answer. Once I have updated the resource function and the new version is accepted in WFR, then I will repost your example using the resource function. – E. Chan-López Jan 22 '24 at 19:40