Can I make a plot with gradient filling?

Question

Bloomberg has a standard plot style for its line plots in which it uses a gradient filling. Actually the way this seems to be constructed is that a gradient from the ymax to ymin is used as the background in the plot area and then the area above the line is set to transparent

enter image description here .

What is the best way to make a plot like that in Mathematica for plotting {x,y} data?

An observation: the color scheme of all the parts of that plot, together, is hideously unattractive to my eyes. And having the background, above the line plot, such a dark color seems a particularly bad choice. — murray, Mar 15 '12 at 00:26
Does anyone else find it odd that a gradient oriented at right angles to this (blending left to right) is as easy as specifying ColorFunction -> (Blend[{Black, Blue}, #1] &), but a top-to-bottom blend is so complex? — Verbeia, Mar 15 '12 at 10:10
I wonder what Edward Tufte would have to say about that chart... — Niki Estner, Mar 15 '12 at 14:01

score 30 · Accepted Answer · edited Oct 07 '12 at 04:21

30

How about this?

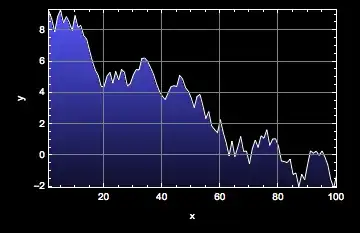
bankerPlot[data_] := ListLinePlot[
  data,
  AxesOrigin -> {0, 0},
  Prolog -> Polygon[Join[data, Reverse[data.DiagonalMatrix[{1, 0}]]],
    VertexColors -> Join[
      Blend[{Black, Blue}, #] & /@ Normalize[data[[All, 2]], Max],
      ConstantArray[Black, Length[data]]
      ]
    ],
  PlotStyle -> White,
  Background -> Black,
  AxesStyle -> White
  ]

bankerData = Transpose[{Range[100], Accumulate[RandomReal[{-1, 1}, 100]] + 10}];
bankerPlot[bankerData]

bankerPlot output

edited Oct 07 '12 at 04:21

J. M.'s missing motivation

124,525
11
401
574

answered Mar 14 '12 at 23:30

ArgentoSapiens

7,780
1
32
49

nice one! I'll leave the question open for a little while but this looks like a winner :) – Mike Honeychurch Mar 14 '12 at 23:41
BTW in my testing I changed from Epilog to Prolog because you lose the solid line otherwise (on my system anyway) – Mike Honeychurch Mar 14 '12 at 23:47
Aha I think we caught that at about the same time. See my latest edit, 7 minutes after my first answer. – ArgentoSapiens Mar 14 '12 at 23:51
+1 for the function name (banker + plot = very sinister). – Jens Mar 15 '12 at 00:27
I like both these methods but I find this one more intuitive than using ParametricPlot. For others it may be different. This one also seems to render faster -- not that the timings are significant enough to be a deciding factor but thought I would mention it anyway. – Mike Honeychurch Mar 15 '12 at 04:22
@ArgentoSapiens great answer. Your model can be migrated to DateListPlot. bankerPlot[data_] := DateListPlot[data, AxesOrigin -> {data[[1, 1]], 0}, Prolog -> Polygon[Join[ data, {DateList[#[[1]]], #[[2]]} & /@
(Reverse[({AbsoluteTime[#[[1]]], #[[2]]} & /@ data).DiagonalMatrix[{1, 0}]])], VertexColors -> Join[Blend[{Black, Blue}, #] & /@ Normalize[data[[All, 2]], Max], ConstantArray[Black, Length[data]]]], PlotStyle -> White, Background -> Black, AxesStyle -> White, FrameStyle -> White, FrameTicks -> {{Automatic, None}, {Automatic, None}}]; – Zviovich Jan 10 '14 at 14:42
koStock = FinancialData["KO", {2013, 1, 1}] ;bankerPlot[koStock] – Zviovich Jan 10 '14 at 14:44

Heike · Answer 2 · 2012-03-14T23:53:00.927

23

For plotting a continuous function, you could do something like this:

f[x_] := (1 + Cos[5 x]/2) Sin[x] 

ParametricPlot[{x, f[x] y}, {x, 0, Pi}, {y, 0, 1},
 PlotPoints -> 30,
 ColorFunction -> (Blend[{Black, Blue, White}, #2] &), Mesh -> None, 
 AspectRatio -> 1/GoldenRatio]

Mathematica graphics

Edit

This method can be used for plotting a list of points as well by interpolating the points first, e.g.

pts1 = RandomReal[10, 100];

interpol = Interpolation[pts1, InterpolationOrder -> 1];

ParametricPlot[{x, interpol[x] y}, {x, 1, Length[pts1]}, {y, 0, 1},
 ColorFunction -> (Blend[{Black, Blue, White}, #2] &), Mesh -> None, 
 AspectRatio -> 1/GoldenRatio]

Mathematica graphics

edited Mar 14 '12 at 23:53

answered Mar 14 '12 at 23:45

Heike

35,858
3
108
157

Hi Heike, what I had in mind was for plotting {x,y} data only. – Mike Honeychurch Mar 14 '12 at 23:48
I like the edit. I can almost replicate @ArgentoSapiens except that PlotStyle->White doesn't seem to be controlling the line colour. – Mike Honeychurch Mar 15 '12 at 00:22
2

@MikeHoneychurch Try BoundaryStyle -> White. – Brett Champion Mar 15 '12 at 03:48
@BrettChampion thanks for that. – Mike Honeychurch Mar 15 '12 at 04:25

score 19 · Answer 3 · answered Mar 15 '12 at 04:16

Here's a modification of Heike's ParametricPlot approach, using textures instead of ColorFunction.

pts1 = RandomReal[10, 100];

interpol = Interpolation[pts1, InterpolationOrder -> 1];

ParametricPlot[{u, interpol[u] v}, {u, 1, Length[pts1]}, {v, 0, 1}, 
 Mesh -> None, AspectRatio -> 1/GoldenRatio, 
 TextureCoordinateFunction -> ({#1, #2} &), 
 PlotStyle -> {Opacity[1], 
   Texture[Table[{{##}} & @@ Blend[{Black, Blue, White}, 1-i], 
      {i, 0, 1, 0.01}]]}]

I'm using a 1-pixel wide Image containing the black-blue-white gradient Heike used. (Actually, it doesn't have an Image head; it's just the ImageData.)

I'm also specifying that I want the texture to correspond to the $x$ and $y$ coordinates instead of the default of $u$ and $v$.

This approach allows us to generalize the gradient to something more complicated, or even an arbitrary image:

ParametricPlot[{u, interpol[u] v}, {u, 1, Length[pts1]}, {v, 0, 1}, 
 Mesh -> None, AspectRatio -> 1/GoldenRatio, 
 TextureCoordinateFunction -> ({#1, #2} &), 
 PlotStyle -> {Opacity[1], Texture[ExampleData[{"TestImage", "Lena"}]]}]

Thanks Brett. I can see where I might want to use this with country's flag as a texture. — Mike Honeychurch, Mar 15 '12 at 04:28

score 17 · Answer 4 · answered Mar 15 '12 at 10:32

17

This is a variant of Argento's answer with the blend on a rectangle in the background rather than creating a polygon that matches the data.

bankerData = 
  Transpose[{Range[100], Accumulate[RandomReal[{-1, 1}, 100]] + 10}];


ListLinePlot[bankerData, Frame -> True, Background -> Black, 
 AxesOrigin -> {0, 0}, PlotRange -> {{1, 100}, {0, 20}}, 
 FrameTicks -> {{Automatic, None}, {Automatic, None}}, 
 PlotRangePadding -> 0, 
 BaseStyle -> {Thick, White, FontFamily -> "Arial", FontSize -> 13}, 
 Filling -> Top, FillingStyle -> Black, Mesh -> None, 
 PlotStyle -> Directive[Thick, White], 
 Prolog -> 
  Polygon[{Scaled[{0, 0}], Scaled[{1, 0}], Scaled[{1, 1}], 
    Scaled[{0, 1}]}, VertexColors -> {Black, Black, Blue, Blue}]]

enter image description here

The disadvantage of my approach is that you need to set PlotRangePadding->0.

answered Mar 15 '12 at 10:32

Verbeia

34,233
9
109
224

hmmm, I like this one the best now :). I usually set PlotRangePadding->0 by default anyway so that would not be an issue for me. – Mike Honeychurch Mar 15 '12 at 19:59
@Verbeia, blue artifacts appear when trying to migrate the model to DateListPlot (to take advantage of FinancialData. koStock = FinancialData["KO", {2013, 1, 1}]; DateListPlot[koStock, AxesOrigin -> {First@koStock[[All, 1]], 0}, Frame -> True, Background -> Black, BaseStyle -> {Thick, White, FontFamily -> "Arial", FontSize -> 13}, Filling -> Top, FillingStyle -> Black, Mesh -> None, PlotStyle -> Directive[Thick, White], Prolog -> Polygon[{Scaled[{0, 0}], Scaled[{1, 0}], Scaled[{1, 1}], Scaled[{0, 1}]}, VertexColors -> {Black, Black, Blue, Blue}], PlotRangePadding -> 0] – Zviovich Jan 10 '14 at 14:46

score 14 · Answer 5 · edited Apr 13 '17 at 12:56

Here is another method that uses the more general gradient background construction I posted as an answer to "How can I set different opacity values for the background of a ListPlot".

This answer is rather late, but I thought it's a good example of how else to use the simple option Prolog -> gradientBackground to create a gradient background:

gradientBackground = 
  With[{bottomColor = Black, topColor = Lighter[Blue]}, 
   Inset[Show[
     Rasterize[
      Graphics[
       Polygon[{{0, 0}, {1, 0}, {1, 1}, {0, 1}}, 
        VertexColors -> {bottomColor, bottomColor, topColor, 
          topColor}], PlotRangePadding -> 0, ImagePadding -> 0], 
      "Image"], AspectRatio -> Full], {Left, Bottom}, {0, 0}, 
    ImageScaled[{1, 1}]]];


bankerData = 
  Transpose[{Range[100], Accumulate[RandomReal[{-1, 1}, 100]] + 10}];

ListLinePlot[
 bankerData,
 Prolog -> gradientBackground,
 PlotRangePadding -> None,
 Frame -> True,
 Axes -> False,
 GridLines -> Automatic,
 PlotStyle -> White,
 FrameLabel -> {"x", "y"},
 Method -> {"GridLinesInFront" -> True},
 PlotRegion -> {{.04, .96}, {.04, .96}},
 Background -> Black,
 Filling -> Top,
 FillingStyle -> Black,
 PlotRange -> All,
 BaseStyle -> {White, FontFamily -> "Arial"}]

banker plot

Mr.Wizard · Answer 6 · 2013-09-05T07:18:41.533

10

While trying to force ColorFunction to work I came up with this:

bankerData = Transpose[{Range[100], Accumulate[RandomReal[{-1, 1}, 100]] + 10}];

bands = 20;

ListLinePlot[Table[{1, i} # & /@ bankerData, {i, 0`, 1`, 1/bands}], 
 Background -> Black, AxesStyle -> White, 
 ColorFunction -> "DeepSeaColors", 
 Filling -> True
]

enter image description here

Adding Mesh -> True gives an idea of how it works:

enter image description here

edited Sep 05 '13 at 07:18

answered Mar 15 '12 at 13:34

Mr.Wizard

271,378
34
587
1,371

score 10 · Answer 7 · answered Mar 15 '12 at 18:02

If you can accept the limitation of a two-color gradient here is another option:

bankerData = 
  Transpose[{Range[100], Accumulate[RandomReal[{-1, 1}, 100]] + 10}];

p1 = ListLinePlot[
       bankerData, 
       ColorFunction -> ({Black, Red} ~Blend~ #2 &),
       Filling -> Axis
     ];

n = Length @ bankerData;

MapAt[Join[# ~Take~ n, Black & /@ # ~Drop~ n] &, p1, {1, -1, 2}]

Mathematica graphics

The index {1, -1, 2} is for the VertexColors list. It works on version 7. If it does not work on your version either find the right index, or use patterns, e.g.:

pos = {#, #2, 2} & @@ Position[p1, VertexColors][[-1]];

MapAt[Join[#~Take~n, Black & /@ #~Drop~n] &, p1, pos]

score 8 · Answer 8 · answered Oct 07 '12 at 00:49

If you are willing to consider a bar chart instead, this can be done with sufficient segments in a "SegmentScaleRectangle" setting for ChartElementFunction. Rendering is a little slow but the result is quite attractive.

testdata = 
  FoldList[0.99 #1 + #2 &, 0., 
   RandomVariate[NormalDistribution[0, 1], 100]];

BarChart[testdata, ChartStyle -> EdgeForm[None], BarSpacing -> 0, 
 PerformanceGoal -> "Speed", 
 ChartElementFunction -> 
  ChartElementDataFunction["SegmentScaleRectangle", "Segments" -> 200,
    "ColorScheme" -> "SunsetColors"]]

enter image description here

This works fine with dark backgrounds: all one needs to do is add
BaseStyle -> White, Background->Black to the options in the BarChart or RectangleChart.

score 3 · Answer 9 · answered Dec 15 '20 at 18:42

New-in-version-12.2.0 styling directive LinearGradientFilling makes the task more straightforward:

data = FinancialData["IBM", "OHLCV", {{2009, 5, 1}, {2010, 4, 30}}];
DateListPlot[data["PathComponent", 4], 
 PlotStyle -> Directive[Thin, GrayLevel[.7]], PlotMarkers -> None, 
 Filling -> Axis, 
 FillingStyle ->
    LinearGradientFilling[{Black, Darker@Darker@Blue, Blue, LightBlue},  Top], 
 PlotTheme -> "Marketing", 
 GridLinesStyle -> Directive[GrayLevel[.4], Dashed], 
 Method -> {"GridLinesInFront" -> True}, ImageSize -> Large]

Can I make a plot with gradient filling?

9 Answers9

Linked

Related