Mathematica gives wrong result while Wolfram|Alpha is correct

Question

Mathematica and Wolfram|Alpha output

Why does Mathematica and Wolfram|Alpha give different results based upon the same code?

I know Wolfram|Alpha's 7.85 is correct.

Looks like a bug to me. Integrate[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], t]; N[(%/.t->2), 20] gives the same wrong result. — Leo Fang, Oct 11 '13 at 22:50
Wolfram Alpha is returning numerical integration because the symbolic integration is timing out. — Greg Hurst, Jun 15 '15 at 14:33

Michael E2 · Accepted Answer · 2013-10-12T16:05:11.820

Artes' guess seems basically right. Here is a way to reach the correct result. First, the antiderivative returned by Mathematica:

i0 = FullSimplify[
       Integrate[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], t],
       t > 0]

(* (2 (Sqrt[16 - 2 I (-5 I + Sqrt[11]) t^2] Sqrt[8 + I (5 I + Sqrt[11]) t^2] (
     5 (-5 I + Sqrt[11]) EllipticE[ArcSin[1/2 t Root[9 - 5 #1^2 + #1^4 &, 4]], 
                                   1/18 (7 - 5 I Sqrt[11])] -
     (11 I + 5 Sqrt[11]) EllipticF[ArcSin[1/2 t Root[9 - 5 #1^2 + #1^4 &, 4]],
                                   1/18 (7 - 5 I Sqrt[11])]) + 
     9/2 t (16 - 20 t^2 + 9 t^4) Root[36 + 10 #1^2 + #1^4 &, 3])) /
       (27 Sqrt[(-5 - I Sqrt[11]) (16 - 20 t^2 + 9 t^4)])  *)

If we add to Pi to the two ArcSin expressions in i0, we get another antiderivative:

i1 = i0 /. a_ArcSin :> Pi + a;

D[i0, t] // FullSimplify[#, t > 0] &
D[i1, t] // FullSimplify[#, t > 0] &

(* Sqrt[16 - 20 t^2 + 9 t^4]
   Sqrt[16 - 20 t^2 + 9 t^4] *)

It turns out that i1 is the continuation of i0:

Plot[{i0, i1}, {t, 0, 2}, 
 PlotStyle -> {Directive[Thick, Blue], Directive[Thick, Red]}]

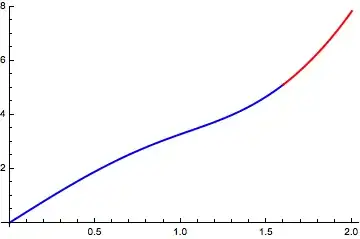
Mathematica graphics

Hence,

(i1 /. t -> 2.) - (i0 /. t -> 0.) 
(* 7.847 - 8.88178*10^-16 I *)

yields the correct (approximate) result.

Such are the pitfalls of elliptic integrals and their symbolic antiderivatives, I suppose. NIntegrate bypasses antiderivatives and estimates the integral from the (real) values of the integrand. It should never encounter such problems.

Further analysis

The plots below show the discontinuities in the EllipticE and EllipticF that lead to the incorrect value for Integrate. The discontinuities violate the conditions necessary to apply the Fundamental Theorem of Calculus (an antiderivative is by definition supposed to be differentiable and therefore continuous).

{x0, x1} = FixedPoint[  (* find the discontinuity *)
  Function[{x}, If[Im@Chop[i0 /. t -> x] != 0, {First[#], x}, {x, Last[#]}]][Mean[#]] &,
  {1.599, 1.6}]

Table[
  With[{part = part, ell = ell}, 
   ContourPlot[
    part[ell[ArcSin[1/2 t Root[9 - 5 #1^2 + #1^4 &, 4]],
             1/18 (7 - 5 I Sqrt[11])]] /. t -> x + I y,
    {x, 0, 2}, {y, -1, 1},
    MaxRecursion -> 3, PlotPoints -> 25,
    AxesOrigin -> {x0, 0}, Axes -> True, 
    AxesStyle -> Directive[Thin, Red], PlotLabel -> part@ell]
   ],
  {ell, {EllipticE, EllipticF}}, {part, {Re, Im}}] // GraphicsGrid

(* {1.5991767250934696`, 1.5991767250934699`} *)

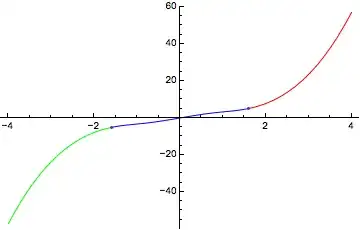
Mathematica graphics

To get the real-valued antiderivative, piece together different branches:

anti = Piecewise[{
    {i0, -x0 <= t <= x0},
    {i0 /. a_ArcSin :> Pi + a, t >= x1},
    {i0 /. a_ArcSin :> -Pi + a, t <= -x1}},
   Indeterminate];

Plot[anti, {t, -4, 4},
 Mesh -> {{-x0, x0}}, MeshShading -> {Green, Blue, Red}]

Mathematica graphics

I have a question -- what an antiderivative is? My guess is the stuff one obtains after integration. — Leo Fang, Oct 12 '13 at 05:14
@LeoFang That's basically right. An antiderivative of a function $f$ is a function $F$ whose derivative $F'$ equals $f$. Also called an (indefinite) integral. It's the stuff returned by Integrate[f[t], t] (with no interval for t). You may know it by a different name. — Michael E2, Oct 12 '13 at 11:24

score 5 · Answer 2 · edited Jun 15 '15 at 14:04

5

This does not really answer the question as to why Mathematica's Integrate yields an apparently wrong answer. This simply states why the two answers are different. It seems Wolfram|Alpha does not attempt to do a symbolic integration (which is what your input asks for) before taking its numerical value. As I stated in my comment, using NIntegrate gives the correct answer similar to Wolfram|Alpha. So, in short, Wolfram|Alpha uses NIntegrate directly. Which is why the following input yields the right answer in Mathematica:

NIntegrate[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], {t, 0, 2}]

7.847

edited Jun 15 '15 at 14:04

J. M.'s missing motivation

124,525
11
401
574

answered Oct 11 '13 at 22:35

RunnyKine

33,088
3
109
176

2

To get an insight what might go wrong see this answer: Why does Integrate declare a convergent integral divergent?. You can see there are elliptic functions as well as ArcSin, together they can produce unwanted imaginary result. There is another problem with real part but I guess they both could be resonably explained (as an inproper phase rule) – Artes Oct 11 '13 at 22:50
@Artes. Thanks for the insight. – RunnyKine Oct 11 '13 at 22:58
Thanks, I guess I'll just use NIntegrate to get a numerical answer in the future. – James83 Oct 12 '13 at 08:24

score 3 · Answer 3 · answered Oct 11 '13 at 23:56

This is not an answer, but comparing the answer with Maple, and also showing step by step integration using Rubi, which might help point to where Mathematica went wrong.

Mathematica Integrate

r = Simplify@Integrate[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], t]

Mathematica graphics

N[r /. t -> 2 - r /. t -> 0, 20]

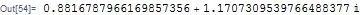
Mathematica graphics

Maple

r:=int(sqrt( (2*t)^2+(4-3*t^2)^2),t=0..2);

Mathematica graphics

evalf[20](r);
7.8469978240383303061+7.9695375019434005093*10^(-20)*I

F in the above is EllipticF and E is EllipticE. So both Maple and Mathematica have the answer in terms of Elliptic functions. To see step by step process, with the hope to better find where the bug happens, I used Rubi:

Rubi 4.2 step by step

ShowSteps = True;
r = Int[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], t]

Mathematica graphics

result = %;
N[result /. t -> 2 - result /. t -> 0, 20]

Mathematica graphics

In one of those steps, the Integrate went wrong. Need more time to analyze.

Up to t==Pi/2 the symbolic integration works. Then it becomes complex — Rojo, Oct 12 '13 at 00:11
Great comparison! Do you have some comment on why Rubi and Mathematica wrong results are the same? My impression was that Rubi is practically independant on Mathematica algorihms for integration. — VividD, May 26 '15 at 18:52

score 3 · Answer 4 · answered Oct 12 '13 at 00:20

3

I observed this behavior while at a training session at Wolfram Headquarters, and there seems to be an issue with using Integers here:

Integrate[Sqrt[(2. t)^2 + (4. - 3. t^2)^2], {t, 0, 2}] // N
(* 7.847 *)

Specifying Real numbers yields the correct result. I can only assume that Wolfram Alpha is performing this calculation with Real numbers as well.

answered Oct 12 '13 at 00:20

bobthechemist

19,693
4
52
138

4

Note that Integrate[Sqrt[(2. t)^2 + (4. - 3. t^2)^2], {t, 0, 2}] returns unevaluated, so the // N basically converts it to an NIntegrate. – Michael E2 Oct 12 '13 at 00:39
Thanks - I missed that. Does this suggest that the problem is with NIntegrate? – bobthechemist Oct 12 '13 at 00:47
3

No, NIntegrate gets it right. The problem is that Integrate takes an algebraic approach, and in this case, the interval $0 \le t \le 2$ seems to cross a branch cut of the antiderivative. – Michael E2 Oct 12 '13 at 01:16

score 2 · Answer 5 · answered Jun 07 '15 at 18:47

Okay, I'm slowly going through the questions involving elliptic integral evaluations. Yet again, none of the software mentioned in this thread have managed to produce a "clean" expression. For the benefit of future readers, here's a tidier closed form for your perusal:

N[2 (7 Sqrt[5] + 2 (10 EllipticE[2 π/3, 11/12] + EllipticF[2 π/3, 11/12])/Sqrt[3])/9, 20]
   7.8469978240383303061

NIntegrate[Sqrt[(2 t)^2 + (4 - 3 t^2)^2], {t, 0, 2}, WorkingPrecision -> 20]
   7.8469978240383303060

Mathematica gives wrong result while Wolfram|Alpha is correct

5 Answers5

Mathematica Integrate

Maple

Rubi 4.2 step by step

Linked