7

Original question

I would like to put a coloured grid behind the following plot:

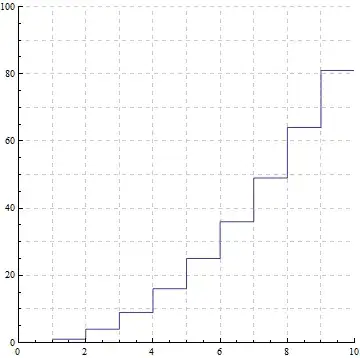
enter image description here

which was generated by:

a = Table[x, {x, 1, 10}];
b = Table[10 x, {x, 1, 10}];
ListLinePlot[{Table[x^2, {x, 1, 10}]}, InterpolationOrder -> 0,
PlotRange -> {{0, 10}, {0, 100}}, GridLines -> {a, b}, GridLinesStyle ->   
Directive[GrayLevel[0.8], Dashed], AspectRatio -> 1]

so that I could shade certain squares of the grid so it looks something like:

enter image description here

for example.

Update1

Using Kuba's code below, it is fairly straightforward to overlay an x^2 shaded plot with an x^3 ListLinePlot using the following code:

data = Table[{x, x^2}, {x, 0, 10}];
ceiling = {#, Ceiling[#2 + 1, 10]} & @@@ data;
floor = {#, Floor[#2, 10]} & @@@ data;
a = Table[x, {x, 1, 10}];
b = Table[10 x, {x, 1, 10}];
c = ListLinePlot[{Table[x^3, {x, 1, 10}]}, InterpolationOrder -> 0, 
PlotRange -> {{0, 10}, {0, 100}}, GridLines -> {a, b}, 
GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], 
AspectRatio -> 1, PlotStyle -> {Thick}];
Show[ListPlot[{data, ceiling, floor}, InterpolationOrder -> 0, 
Joined -> True, AspectRatio -> 1, Filling -> (2 -> {3}), 
GridLines -> {Range[10], Range[0, 100, 10]}, 
GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], 
PlotStyle -> {None, None, None}], c]

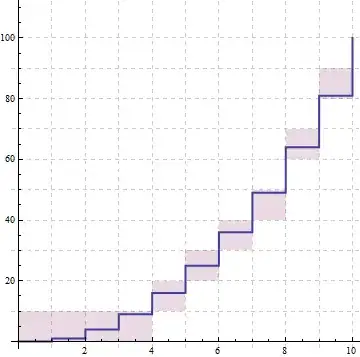
which generates:

enter image description here

without too much fiddling. Is there a similarly straightforward way of showing a shaded x^3 plot & ListLinePlot x^2 without running into problems with the dimensions of the grid (without fiddling around with the dimensions each time)?

Update2

Thanks to Kuba's code:

enter image description here

with:

lineData[f_, max_, min_: 0] := Table[{x, f[x]}, {x, min, max}];
shadeData[f_, max_, min_: 0] := 
Transpose[{{#, Ceiling[#2 + 1, 10]}, {#, Floor[#2, 10]}} & @@@ 
Table[{x, f[x]}, {x, min, max}]]

With[{stdOpt = {InterpolationOrder -> 0, 
GridLines -> {Range[10], Range[0, 300, 10]}, 
GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], 
Joined -> True, AspectRatio -> 1}}, 
ListPlot[{lineData[#^2 &, 10], ##} & @@ shadeData[#^3 &, 10], 
Filling -> (2 -> {3}), PlotStyle -> {Thick, None, None}, stdOpt, 
PlotRange -> {{0, 10}, {0, 100}},

Epilog -> {Red, Opacity[0.5], Rectangle[{1, 10}, {2, 20}], Blue, 
Opacity[0.5], Rectangle[{2, 40}, {3, 50}]}

]]

Update3

Having some fun with it: enter image description here

with:

shadeData[f_, max_, min_: 0] := 
Transpose@Table[{{x, Ceiling[f[x] + If[FractionalPart[f[x]] == 0.5, 0.5, 0], 1]},
{x, Floor[f[x], 1]}}, {x, min, max}]

Animate[Quiet[With[{stdOpt = {InterpolationOrder -> 0, GridLines -> {Range[-10, 28,
1], Range[-10, 14]}, GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], 
Joined -> True, AspectRatio -> 0.25}}, ListPlot[shadeData[(Sin[# + n])*10 &, 28], 
Filling -> (2 -> {1}), FillingStyle -> Directive[Opacity[0.5], Orange], 
PlotStyle -> {None, None, None}, stdOpt, Axes -> False, Frame -> False, 
ImageSize -> 600, PlotRange -> {{0, 24}, {-10, 10}}]]], {n, 0, 2 \[Pi]}, 
AnimationDirection -> Forward, AnimationRate -> 0.5]

and

enter image description here

...etc :)

martin
  • 8,678
  • 4
  • 23
  • 70
  • You will need to use Graphics and Rectanlge to build this directly, instead of using an existing plotting function. Have you tried this route already? Take a look here. – Szabolcs Nov 20 '13 at 19:02
  • I have tried positioning rectangles behind the plot using Inset, but it proved to be difficult to position them :/ – martin Nov 20 '13 at 19:04
  • 1
    You don't need Inset because Rectangle is a graphics primitive. Inset is for putting things that are not graphics primitives into Graphics. Just use a Table to generate the list of Rectangles with appropriate coordinates. – Szabolcs Nov 20 '13 at 19:07
  • OK thanks - I'll give that a go :) – martin Nov 20 '13 at 19:09
  • You may need to use this for better looks after all the other pieces came together. – Szabolcs Nov 20 '13 at 19:11
  • Tried Show, & ArrayPlot[Table[GCD[i, j], {i, 10}, {j, 10}]] ... no good! - Will go back to your original suggestion - thanks for the other link. – martin Nov 20 '13 at 19:13

1 Answers1

12

There is no need to use grapics primitives:

data = Table[{x, x^2}, {x, 0, 10}];
ceiling = {#, Ceiling[#2 + 1, 10]} & @@@ data;
floor = {#, Floor[#2, 10]} & @@@ data;

ListPlot[{data, ceiling, floor}, InterpolationOrder -> 0, Joined -> True, AspectRatio -> 1,
   Filling -> (2 -> {3}), GridLines -> {Range[10], Range[0, 100, 10]}, 
   GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], PlotStyle -> {Thick, None, None}]

enter image description here

Response to the edit with a general approach. We don't need Show. I've also added single Rectangle with Epilog as you asked.

lineData[f_, max_, min_: 0] := Table[{x, f[x]}, {x, min, max}];
shadeData[f_, max_, min_: 0] := Transpose @
  Table[{{x, Ceiling[f[x] + If[FractionalPart[f[x]] == 0, 1, 0], 10]}, 
         {x, Floor[f[x], 10]}}
       , {x, min, max}]

With[{stdOpt = {InterpolationOrder -> 0, GridLines -> {Range[10], Range[0, 300, 10]}, 
      GridLinesStyle -> Directive[GrayLevel[0.8], Dashed], Joined -> True,
      AspectRatio -> 1}},

 ListPlot[{lineData[#^2 &, 6], ##} & @@ shadeData[#^3 &, 6], 
          Filling -> (2 -> {3}), PlotStyle -> {Thick, None, None}, stdOpt, 
          Epilog -> Rectangle[{1, 50}, {2, 60}]] ]

enter image description here

Kuba
  • 136,707
  • 13
  • 279
  • 740
  • @Blackbird Thanks :) – Kuba Nov 20 '13 at 19:34
  • @Kuba - Thanks! Great. Now if I wanted to colour, say, x^3, and ListLinePlot x^2, I suppose I would use Show? Just having a little trouble with scaling when I do that :/ – martin Nov 20 '13 at 19:37
  • @Kuba, please see update - want to keep it fairly flexible if poss. – martin Nov 20 '13 at 19:45
  • @Kuba, also(!) (though not as important) is it possible to use the same floor/ceiling concept with a ListPlot using coordinates - thereby letting me choose which squares to shade, independent of ListLinePlot? – martin Nov 20 '13 at 19:50
  • 1
    @martin for manually choosen rectangles there is no purpose for usage of Floor. Is the edit ok? ;) – Kuba Nov 20 '13 at 19:59
  • @Kuba, thank you very much for the time you spent on this - it is exactly what I was after :) I will have a play! – martin Nov 20 '13 at 20:08
  • @martin Epilog-> {...} and in ... you can put whatever you want that would work in Graphics. – Kuba Nov 20 '13 at 20:22
  • @martin you probably wanted to edit the question not th answer :) – Kuba Nov 20 '13 at 20:41
  • 1
    @martin use this: shadeData[f_, max_, min_: 0] := Transpose@ Table[{{x, Ceiling[f[x] + If[FractionalPart[f[x]] == 0, 1, 0], 10]}, {x, Floor[f[x], 10]}}, {x, min, max}]. Also, please delete your previous comments that are no longer important ;) – Kuba Nov 20 '13 at 22:06